Lý thuyết hàm số mũ, hàm số lôgarit
Tổng hợp lý thuyết hàm số mũ và hàm số lôgarit ngắn gọn, dễ hiểu
1. Định nghĩa
Hàm số mũ là hàm số có dạng \(y = {a^x}\), hàm số lôgarit là hàm số có dạng \(y = {\log _a}x\) ( với cơ số a dương khác 1).
2. Tính chất của hàm số mũ \(y = {a^x}\) \(( a > 0, a\ne 1)\).
- Tập xác định: \(\mathbb{R}\).
- Đạo hàm: \(∀x ∈\mathbb{R},y'= a^x \ln a\).
- Chiều biến thiên
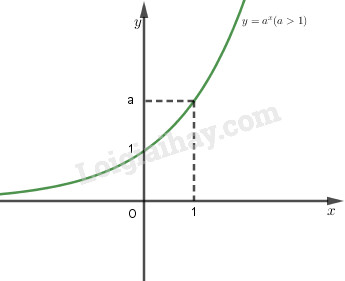
+) Nếu \(a> 1\) thì hàm số luôn đồng biến
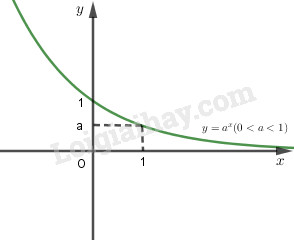
+) Nếu \(0< a < 1\) thì hàm số luôn nghịch biến
- Tiệm cận: trục \(Ox\) là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành \((y = {a^x} >0 \, \forall x)\), và luôn cắt trục tung tại điểm \(( 0;1)\) và đi qua điểm \((1;a)\).
3. Tính chất của hàm số lôgarit \(y = {\log _a}x\) \((a> 0, a\ne1)\).
- Tập xác định: \((0; +∞)\).
- Đạo hàm \(∀x ∈ (0; +∞),y'= \dfrac{1}{x\ln a}\).
- Chiều biến thiên:
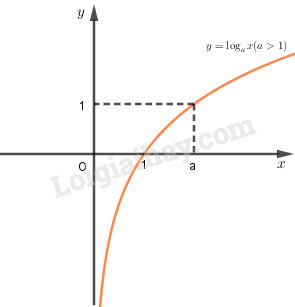
+) Nếu \(a> 1\) thì hàm số luôn đồng biến
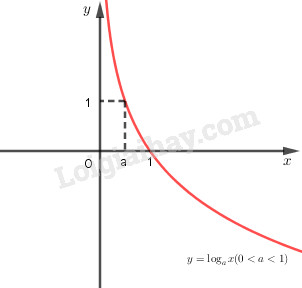
+) Nếu \(0< a < 1\) thì hàm số luôn nghịch biến
- Tiệm cận: Trục \(Oy\) là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm \((1;0)\) và đi qua điểm \((a;1)\).
4. Chú ý
- Nếu \(a > 1\) thì \(\ln a > 0\), suy ra \((a^x)'>0 \, \, \forall x\) và \({({\log_a}^x)}\; > 0,\;\;\forall x{\rm{ }} > 0;\)
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu \(0 < a< 1\) thì \(\ln a < 0\), \(({a^x})' < 0\) và \({({\log_a}^x)}\; < 0,\;\;\forall x{\rm{ }} > 0;\) ; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
\( (\ln |x|)'= \dfrac{1}{x}, ∀x \ne 0\) và \((\log _a|x|)' = \frac{1}{{x\ln a}},{\rm{ }}\forall x \ne 0.\)

5. Bài tập về hàm số mũ, hàm số lôgarit
Bài 1. Chọn mệnh đề đúng:
A. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) đồng biến nếu \(a > 1\).
B. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) nghịch biến nếu \(0 < a < 1\).
C. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) đồng biến nếu \(0 < a < 1\).
D. Hàm số \(y = {a^{ - x}}\left( {0 < a \ne 1} \right)\) luôn nghịch biến trên \(R\).
Lời giải: Ta có:
Hàm số $y=a^{-x}$ nghịch biến khi $a>1$ nên các đáp án B, D đều sai.
\(y = {a^{ - x}} = \dfrac{1}{{{a^x}}} = {\left( {\dfrac{1}{a}} \right)^x}\left( {0 < a \ne 1} \right)\) nên hàm số đồng biến nếu \(\dfrac{1}{a} > 1 \Leftrightarrow 0 < a < 1\).
Chọn đáp án C.
Bài 2. Chọn mệnh đề đúng:
A. Đồ thị hàm số \(y = {2^x}\) trùng với đồ thị hàm số \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\)
B. Đồ thị hàm số \(y = {2^x}\) trùng với đồ thị hàm số \(y = {2^{ - x}}\).
C. Đồ thị hàm số \(y = {2^x}\) đối xứng với đồ thị hàm số \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) qua trục hoành
D. Đồ thị hàm số \(y = {2^x}\) đối xứng với đồ thị hàm số \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) qua trục tung.
Lời giải: Ta có: \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}} = \dfrac{1}{{{{\left( {\dfrac{1}{2}} \right)}^x}}} = \dfrac{1}{{\dfrac{1}{{{2^x}}}}} = {2^x}\) nên hai hàm số \(y = {2^x}\) và \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\) là một. Do đó chúng có chung đồ thị.
Chọn đáp án A.
Bài 3. Đồ thị hàm số dưới đây là của hàm số nào?

A. \(y = {2^{ - x}}\)
B. \(y = {\left( {\dfrac{1}{2}} \right)^{ - x}}\)
C. \(y = - {\left( {\dfrac{1}{2}} \right)^x}\)
D. \(y = - {2^x}\)
Lời giải: Quan sát đồ thị ta thấy nó nằm hoàn toàn phía dưới trục hoành nên loại A và B.
Lại có, đồ thị hàm số đi qua điểm \(\left( { - 1; - 2} \right)\) nên thay tọa độ điểm này vào các hàm số C và D ta được đáp án C.
Chọn đáp án C.
Bài 4. Hàm số \(y = {2^{\ln x + {x^2}}}\) có đạo hàm là
A. \(\left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}\)
B. \(\left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2\)
C. \(\dfrac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\)
D. \(\left( {\dfrac{1}{x} + 2x} \right)\dfrac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\)
Lời giải: Có $y = {2^{\ln x + {x^2}}} \Rightarrow y' = \left( {\dfrac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2$
Chọn đáp án B.
Bài 5. Gọi $(C)$ là đồ thị hàm số \(y = \log x\). Tìm khẳng định đúng?
A. Đồ thị $(C)$ có tiệm cận đứng
B. Đồ thị $(C)$ có tiệm cận ngang.
C. Đồ thị $(C)$ cắt trục tung.
D. Đồ thị $(C)$ không cắt trục hoành.
Lời giải:
- Đồ thị hàm số \(y = \log x\) nhận trục tung là tiệm cận đứng.
- Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm $(1;0)$ nên các đáp án B,C,D đều sai
Chọn đáp án A.
Bài 6. Cho $a, b$ là các số thực, thỏa mãn \(0 < a < 1 < b\), khẳng định nào sau đây là đúng?
A. \({\log _b}a + {\log _a}b < 0\)
B. \({\log _b}a > 1\)
C. \({\log _a}b > 0\)
D. \({\log _a}b + {\log _b}a \ge 2\)
Lời giải: Ta có: \(0 < a < 1\) nên hàm số \(y = {\log _a}x\) nghịch biến, do đó \(b > 1\) nên \({\log _a}b < {\log _a}1 = 0\).
Vì \(b > 1\) nên hàm số \(y = {\log _b}x\) đồng biến, do đó \(a < 1\) nên \({\log _b}a < {\log _b}1 = 0\).
Vậy \({\log _a}b < 0;{\log _b}a < 0 \Rightarrow {\log _a}b + {\log _b}a < 0\).
Chọn đáp án A.
Bài 7. Tìm tập xác định D của hàm số \(y = {\log _{\sqrt 2 }}\left( {\dfrac{{ - 3}}{{2 - 2x}}} \right)\).
A. \(D = ( - \infty ;1)\)
B. \(D = {\rm{[}}1; + \infty )\)
C. \(D = ( - \infty ;1]\)
D. \(D = (1; + \infty )\)
Lời giải: Điều kiện : \(\dfrac{{ - 3}}{{2 - 2x}} > 0 \Leftrightarrow 2 - 2x < 0 \Leftrightarrow x > 1.\)
Chọn đáp án D.
Bài 8. Đạo hàm hàm số \(y = {\log _{2018}}\left( {2018x + 1} \right)\) là:
A. \(\dfrac{1}{{x\ln 2018}}\)
B. \(\dfrac{{2018}}{{2018\left( {x + 1} \right)\ln 2018}}\)
C. \(\dfrac{1}{{\left( {2018x + 1} \right)\ln 2018}}\)
D. \(\dfrac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\)
Lời giải: Ta có:
\(\left[ {{{\log }_{2018}}\left( {2018x + 1} \right)} \right]' = \dfrac{{\left( {2018x + 1} \right)'}}{{\left( {2018x + 1} \right)\ln 2018}} = \dfrac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\)
Chọn đáp án D.













Danh sách bình luận