Copyright © 2021 loigiaihay.com
CHƯƠNG 1. ĐA THỨC
Bài 1. Đơn thức
Bài 2. Đa thức
Bài 3. Phép cộng và phép trừ đa thức
Luyện tập chung trang 17
Bài 4. Phép nhân đa thức
Bài 5. Phép chia đa thức cho đơn thức
Luyện tập chung trang 25
Bài tập cuối chương 1
CHƯƠNG 2. HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG
Bài 6. Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Bài 7. Lập phương của một tổng. Lập phương của một hiệu
Bài 8. Tổng và hiệu hai lập phương
Luyện tập chung trang 40
Bài 9. Phân tích đa thức thành nhân tử
Luyện tập chung trang 45
Bài tập cuối chương 2
CHƯƠNG 3. TỨ GIÁC
Bài 10. Tứ giác
Bài 11. Hình thang cân
Luyện tập chung trang 56
Bài 12. Hình bình hành
Luyện tập chung trang 62
Bài 13. Hình chữ nhật
Bài 14. Hình thoi và hình vuông
Luyện tập chung trang 73
Bài tập cuối chương 3
CHƯƠNG 4. ĐỊNH LÍ THALES
Bài 15. Định lí Thales trong tam giác
Bài 16. Đường trung bình của tam giác
Bài 17. Tính chất đường phân giác của tam giác
Luyện tập chung trang 87
Bài tập cuối chương 4
CHƯƠNG 5. DỮ LIỆU VÀ BIỂU ĐỒ
Bài 18. Thu thập và phân loại dữ liệu
Bài 19. Biểu diễn dữ liệu bằng bảng, biểu đồ
Bài 20. Phân tích dữ liệu thống kê dựa vào biểu đồ
Luyện tập chung trang 106
Bài tập cuối chương 5
CHƯƠNG 6. PHÂN THỨC ĐẠI SỐ
Bài 21. Phân thức đại số
Bài 22. Tính chất cơ bản của phân thức đại số
Luyện tập chung trang 13
Bài 23. Phép cộng và phép trừ phân thức đại số
Bài 24. Phép nhân và phép chia phân thức đại số
Luyện tập chung trang 23
Bài tập cuối chương 6
CHƯƠNG 7. PHƯƠNG TRÌNH BẬC NHẤT VÀ HÀM SỐ BẬC NHẤT
Bài 25. Phương trình bậc nhất một ẩn
Bài 26. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 37
Bài 27. Khái niệm hàm số và đồ thị của hàm số
Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài 29. Hệ số góc của đường thẳng
Luyện tập chung trang 55
Bài tập cuối chương 7
CHƯƠNG 8. MỞ ĐẦU VỀ TÍNH XÁC SUẤT CỦA BIẾN CỐ
Bài 30. Kết quả có thể và kết quả thuận lợi
Bài 31. Cách tính xác suất của biến cố bằng tỉ số
Bài 32. Mối liên hệ giữa xác suất thực nghiệm với xác suất ứng dụng
Luyện tập chung trang 74
Bài tập cuối chương 8
CHƯƠNG 9. TAM GIÁC ĐỒNG DẠNG
Bài 33. Hai tam giác đồng dạng
Bài 34. Ba trường hợp đồng dạng của hai tam giác
Luyện tập chung trang 91
Bài 35. Định lí Pythagore và ứng dụng
Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
Bài 37. Hình đồng dạng
Luyện tập chung trang 108
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 38. Hình chóp tam giác đều
Bài 39. Hình chóp tứ giác đều
Luyện tập chung trang 121
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Công thức lãi kép
Thực hiện tính toán trên đa thức với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm GeoGebra
Phân tích đặc điểm khí hậu Việt Nam
Một vài ứng dụng của hàm số bậc nhất trong tài chính
Ứng dụng định lí Thalès, định lí Pythagore và tam giác đồng dạng để đo chiều cao, khoảng cách
Thực hành tính toán trên phân thức đại số và vẽ đồ thị hàm số với phần mềm GeoGebra
Mô tả thí nghiệm ngẫu nhiên với phần mềm Excel
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Chứng minh hình bình hành Toán 9 có đáp án
Trắc nghiệm Chứng minh hình bình hành
11 câu hỏi
30 phút
Trắc nghiệm
-
A.
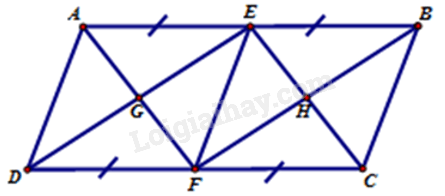
6 hình bình hành
-
B.
5 hình bình hành
-
C.
4 hình bình hành
-
D.
3 hình bình hành
Câu 2 :
Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
-
A.
DE = BF
-
B.
DE > BF
-
C.
DE < BF
-
D.
DE = EB
Câu 3 :
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
-
A.
Hình thang
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Câu 4 :
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu sai.
-
A.
BH // CD
-
B.
CH // BD
-
C.
BH = CD
-
D.
HB = HC
Câu 5 :
Cho tứ giác ABCD. Gọi E, F lần lượt là giao điểm của AB và CD, AD và BC; M, N, P, Q lần lượt là các điểm sao cho MN // AC; \(MN = \frac{1}{2}AC\); PQ // AC; \(PQ = \frac{1}{2}AC\). Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
-
A.
Hình bình hành
-
B.
Hình thang vuông
-
C.
Hình thang cân
-
D.
Hình thang
Câu 6 :
Cho hình bình hành ABCD. Trên đường chéo BD lấy hai điểm E và F sao cho \(BE = DF < \frac{1}{2}B{{D}}\). Chọn khẳng định đúng.
-
A.
FA = CE
-
B.
FA < CE
-
C.
FA > CE
-
D.
Chưa kết luận được
Câu 7 :
Cho tam giác ABC. Gọi D, M, E theo thứ tự là trung điểm của AB, BC, CA sao cho ME // AB; \(ME = \frac{{AB}}{2}\). Tứ giác ADME là:
-
A.
Hình thang
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Câu 8 :
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB và CD; M, N, P, Q lần lượt là thuộc các cạnh AF, EC, BF, DE và \(FN = \frac{1}{2}DE;FN//DE\); \(EM = \frac{1}{2}BF;EM//BF\) . Khi đó MNPQ là hình gì? Chọn đáp án đúng nhất.
-
A.
Hình bình hành
-
B.
Hình thang vuông
-
C.
Hình thang cân
-
D.
Hình thang
Câu 9 :
Cho hình bình hành \(ABCD\). Gọi \(H, K\) lần lượt là hình chiếu của \(A, C\) trên đường thẳng \(BD\). Khẳng định nào sau đây là đúng?
-
A.
\(AH=HC\);
-
B.
\(AH\parallel BC\);
-
C.
\(AH=AK\);
-
D.
\(AHCK\) là hình bình hành.
Câu 10 :
Cho tứ giác \(ABCD\). Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(CD\); \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm các cạnh \(AF\), \(EC\), \(BF\), \(DE\) và \(FN = \frac{1}{2}DE;\,FN\parallel DE\); \(EM = \frac{1}{2}BF;\,EM\parallel BF\). Khi đó \(MNPQ\) là hình gì? Khẳng định nào sau đây là đúng nhất?
-
A.
Hình bình hành
-
B.
Hình thang vuông
-
C.
Hình thang cân
-
D.
Hình thang
Câu 11 :
Cho tam giác \(ABC\) với ba trung tuyến \(AI, BD, CE\) đồng quy tại \(G\) sao cho \(ED\parallel BC;\,ED = \frac{1}{2}BC\). \(M\) và \(N\) lần lượt là các điểm của \(GC\) và \(GB\) và \(MN\parallel BC;\,MN = \frac{1}{2}BC\). Tứ giác \(MNED\) là hình gì?
-
A.
Hình chữ nhật
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
CÁC BÀI TẬP KHÁC
