Copyright © 2021 loigiaihay.com
CHƯƠNG 1. ĐA THỨC
Bài 1. Đơn thức
Bài 2. Đa thức
Bài 3. Phép cộng và phép trừ đa thức
Luyện tập chung trang 17
Bài 4. Phép nhân đa thức
Bài 5. Phép chia đa thức cho đơn thức
Luyện tập chung trang 25
Bài tập cuối chương 1
CHƯƠNG 2. HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG
Bài 6. Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Bài 7. Lập phương của một tổng. Lập phương của một hiệu
Bài 8. Tổng và hiệu hai lập phương
Luyện tập chung trang 40
Bài 9. Phân tích đa thức thành nhân tử
Luyện tập chung trang 45
Bài tập cuối chương 2
CHƯƠNG 3. TỨ GIÁC
Bài 10. Tứ giác
Bài 11. Hình thang cân
Luyện tập chung trang 56
Bài 12. Hình bình hành
Luyện tập chung trang 62
Bài 13. Hình chữ nhật
Bài 14. Hình thoi và hình vuông
Luyện tập chung trang 73
Bài tập cuối chương 3
CHƯƠNG 4. ĐỊNH LÍ THALES
Bài 15. Định lí Thales trong tam giác
Bài 16. Đường trung bình của tam giác
Bài 17. Tính chất đường phân giác của tam giác
Luyện tập chung trang 87
Bài tập cuối chương 4
CHƯƠNG 5. DỮ LIỆU VÀ BIỂU ĐỒ
Bài 18. Thu thập và phân loại dữ liệu
Bài 19. Biểu diễn dữ liệu bằng bảng, biểu đồ
Bài 20. Phân tích dữ liệu thống kê dựa vào biểu đồ
Luyện tập chung trang 106
Bài tập cuối chương 5
CHƯƠNG 6. PHÂN THỨC ĐẠI SỐ
Bài 21. Phân thức đại số
Bài 22. Tính chất cơ bản của phân thức đại số
Luyện tập chung trang 13
Bài 23. Phép cộng và phép trừ phân thức đại số
Bài 24. Phép nhân và phép chia phân thức đại số
Luyện tập chung trang 23
Bài tập cuối chương 6
CHƯƠNG 7. PHƯƠNG TRÌNH BẬC NHẤT VÀ HÀM SỐ BẬC NHẤT
Bài 25. Phương trình bậc nhất một ẩn
Bài 26. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 37
Bài 27. Khái niệm hàm số và đồ thị của hàm số
Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài 29. Hệ số góc của đường thẳng
Luyện tập chung trang 55
Bài tập cuối chương 7
CHƯƠNG 8. MỞ ĐẦU VỀ TÍNH XÁC SUẤT CỦA BIẾN CỐ
Bài 30. Kết quả có thể và kết quả thuận lợi
Bài 31. Cách tính xác suất của biến cố bằng tỉ số
Bài 32. Mối liên hệ giữa xác suất thực nghiệm với xác suất ứng dụng
Luyện tập chung trang 74
Bài tập cuối chương 8
CHƯƠNG 9. TAM GIÁC ĐỒNG DẠNG
Bài 33. Hai tam giác đồng dạng
Bài 34. Ba trường hợp đồng dạng của hai tam giác
Luyện tập chung trang 91
Bài 35. Định lí Pythagore và ứng dụng
Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
Bài 37. Hình đồng dạng
Luyện tập chung trang 108
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 38. Hình chóp tam giác đều
Bài 39. Hình chóp tứ giác đều
Luyện tập chung trang 121
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Công thức lãi kép
Thực hiện tính toán trên đa thức với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm GeoGebra
Phân tích đặc điểm khí hậu Việt Nam
Một vài ứng dụng của hàm số bậc nhất trong tài chính
Ứng dụng định lí Thalès, định lí Pythagore và tam giác đồng dạng để đo chiều cao, khoảng cách
Thực hành tính toán trên phân thức đại số và vẽ đồ thị hàm số với phần mềm GeoGebra
Mô tả thí nghiệm ngẫu nhiên với phần mềm Excel
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Cách giải phương trình đưa về dạng ax + b = 0 Toán 9 có đáp án
Trắc nghiệm Cách giải phương trình đưa về dạng ax + b = 0
17 câu hỏi
30 phút
Trắc nghiệm
Câu 1 :
Nghiệm của phương trình \(3x - 6 = 0\) là:
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = \frac{{ - 1}}{2}\)
-
C.
\(x = 2\)
-
D.
\(x = - 2\)
Câu 2 :
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
A.
\(a + b = 21\)
-
B.
\(a + b = 23\)
-
C.
\(a + b = 20\)
-
D.
\(a + b = 24\)
Câu 3 :
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
-
A.
\( - 24\)
-
B.
\(24\)
-
C.
\( - 16\)
-
D.
16
Câu 4 :
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = - \frac{1}{2}\)
-
C.
\(x = \frac{1}{4}\)
-
D.
\(x = \frac{{ - 1}}{4}\)
Câu 5 :
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
-
A.
\({x_0} < 0\)
-
B.
\({x_0} < - 1\)
-
C.
\({x_0} > 0\)
-
D.
\({x_0} > 1\)
Câu 6 :
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
-
A.
\(x = 1\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 2\)
Câu 7 :
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
-
A.
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
-
B.
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
-
C.
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
-
D.
Cả phương trình (1) và phương trình (2) đều có một nghiệm
Câu 8 :
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
-
A.
Nghiệm của phương trình là một chia hết cho 5
-
B.
Nghiệm của phương trình là một số chia hết cho 2
-
C.
Nghiệm của phương trình là một chia hết cho 4
-
D.
Nghiệm của phương trình là một số nguyên tố
Câu 9 :
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
-
A.
\(m \ne \frac{4}{3}\)
-
B.
\(m = \frac{4}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m \ne \frac{3}{4}\)
-
A.
\(x = - 2\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Câu 11 :
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
-
A.
\(a = 7\)
-
B.
\(a = - 7\)
-
C.
\(a = \frac{1}{7}\)
-
D.
\(a = \frac{{ - 1}}{7}\)
Câu 12 :
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
Không có nghiệm nào
-
D.
Có vô số nghiệm
Câu 13 :
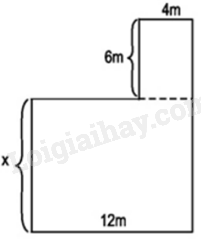
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:
-
A.
11m
-
B.
12m
-
C.
13m
-
D.
14m
Câu 14 :
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
-
A.
\(48 = 32\left( {x - 1} \right)\)
-
B.
\(48x = 32\left( {1 - x} \right)\)
-
C.
\(48x = 32\left( {x - 1} \right)\)
-
D.
\(48x = 32\left( {x + 1} \right)\)
Câu 15 :
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m \in \left\{ {1;2} \right\}\)
-
D.
\(m = 0\)
Câu 16 :
Phương trình \(x - 8 = x - 5\). Khẳng định nào sau đây đúng?
-
A.
Phương trình đã cho có vô số nghiệm.
-
B.
Phương trình đã cho vô nghiệm.
-
C.
Phương trình đã cho có một nghiệm.
-
D.
Phương trình đã cho có hai nghiệm.
Câu 17 :
Phương trình \(3x - 10 = 2x - 12\) có bao nhiêu nghiệm?
-
A.
0
-
B.
1
-
C.
2
-
D.
Vô số nghiệm
