Trắc nghiệm Trường hợp đồng dạng g - g Toán 9 có đáp án
Trắc nghiệm Trường hợp đồng dạng g - g
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}\) , \(\widehat{C}=\widehat{F}\) thì
-
A.
\(\Delta ABC\backsim \Delta DEF\) .
-
B.
\(\Delta CAB\backsim \Delta DEF\) .
-
C.
\(\Delta ABC\backsim \Delta DFE\) .
-
D.
\(\Delta CAB \backsim \Delta DFE\)
Nếu \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}={{70}^{\circ }}\) , \(\widehat{C}={{60}^{\circ }}\) , \(\widehat{E}={{50}^{\circ }}\) , \(\widehat{F}={{70}^{\circ }}\) thì
-
A.
\(\Delta ACB\,\,\backsim \,\,\Delta FED\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta FED\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta DEF\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta DFE\) .
Cho \(\Delta ABC\,\backsim \,\Delta {A}'{B}'{C}'\) (g – g ). Khẳng định nào sau đây đúng
-
A.
\(\widehat{A}=\widehat{{{B}'}}\) .
-
B.
\(AB={A}'{B}'\) .
-
C.
\(\frac{AB}{AC}=\frac{{A}'{B}'}{{A}'{C}'}\) .
-
D.
\(\frac{AB}{AC}=\frac{{A}'{C}'}{{A}'{B}'}\) .
-
A.
\(\Delta HIG\backsim \Delta DEF\) .
-
B.
\(\Delta IGH\backsim \Delta DEF\) .
-
C.
\(\Delta HIG\backsim \Delta DFE\) .
-
D.
\(\Delta HGI\backsim \Delta DEF\) .
Hai tam giác đồng dạng với nhau theo trường hợp góc – góc nếu
-
A.
ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
-
B.
hai góc của tam giác này lần lượt bằng hai góc của tam giác kia.
-
C.
có hai cặp cạnh tương ứng bằng nhau.
-
D.
hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau.
Nếu \(\Delta ABC\) và \(\Delta MNP\) có \(\widehat{A}=\widehat{N}\) ; \(\widehat{B}=\widehat{M}\) thì
-
A.
\(\Delta ABC\backsim \,\Delta MNP\) .
-
B.
\(\Delta CAB\backsim \Delta NMP\) .
-
C.
\(\Delta ABC\backsim \Delta PMN\) .
-
D.
\(\Delta ABC\backsim \Delta NMP\) .
Nếu \(\Delta MNP\) và \(\Delta DEF\) có \(\widehat{M}=\widehat{D}=90{}^\circ \) , \(\widehat{P}=50{}^\circ \) . Để \(\Delta MNP\,\backsim \,\Delta DEF\) thì cần thêm điều kiện
-
A.
\(\widehat{E}=50{}^\circ \) .
-
B.
\(\widehat{F}=60{}^\circ \) .
-
C.
\(\widehat{F}=40{}^\circ \) .
-
D.
\(\widehat{E}=40{}^\circ \)
Nếu \(\Delta DEF\) và \(\Delta SRK\) có \(\widehat{D}=70{}^\circ \) ; \(\widehat{E}=60{}^\circ \) ; \(\widehat{S}=70{}^\circ \) ; \(\widehat{K}=50{}^\circ \) thì
-
A.
\(\frac{DE}{SR}=\frac{DF}{SK}=\frac{EF}{RK}\) .
-
B.
\(\frac{DE}{SR}=\frac{DF}{RK}=\frac{EF}{SK}\) .
-
C.
\(\frac{DE}{SR}=\frac{DF}{SR}=\frac{EF}{RK}\) .
-
D.
\(\frac{DE}{RK}=\frac{DF}{SK}=\frac{EF}{SR}\)
Cho hình thang \(ABCD\) \(\left( {AB\,{\rm{//}}\,CD} \right)\), \(O\) là giao điểm hai đường chéo \(AC\) và \(BD\). Khẳng định nào sau đây đúng
-
A.
\({\rm{\Delta }}OAB \backsim \,\Delta ODC\).
-
B.
\({\rm{\Delta }}CAB \backsim {\rm{\Delta }}CDA\).
-
C.
\({\rm{\Delta }}OAB \backsim {\rm{\Delta }}OCD\).
-
D.
\({\rm{\Delta }}OAD \backsim {\rm{\Delta }}OBC\).
Cho hình thang \(ABCD\,\,\left( {AB\,{\rm{//}}\,CD} \right)\), \(\widehat {ADB} = \widehat {BCD}\), \(AB = 2\,{\rm{cm}}\), \(BD = \sqrt 5 \,{\rm{cm}}\). Độ dài đoạn thẳng \(CD\) là

-
A.
\(2\sqrt 5 \,{\rm{cm}}\).
-
B.
\(\sqrt 5 - 2\,{\rm{cm}}\).
-
C.
\(\frac{{\sqrt 5 }}{2}\,{\rm{cm}}\).
-
D.
\(2,5\,{\rm{cm}}\).
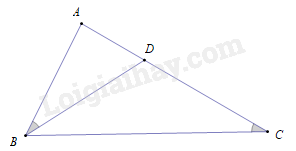
Cho hình vẽ, biết \(\widehat {ACB} = \widehat {ABD}\), \(AB = 3\,{\rm{cm}}\), \(AC = 4,5\,{\rm{cm}}\). Độ dài đoạn thẳng \(AD\) là
-
A.
\(2\,{\rm{cm}}\).
-
B.
\(2,5\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(1,5\,{\rm{cm}}\).
\(\Delta ABC\) vuông tại \(A\) có \(\widehat B = 60^\circ \), \(BD\) là phân giác \(\widehat B\), \(AC = 18\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(12\,{\rm{cm}}\).
-
B.
\(10\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(8\,{\rm{cm}}\).