Copyright © 2021 loigiaihay.com
CHƯƠNG 1. ĐA THỨC
Bài 1. Đơn thức
Bài 2. Đa thức
Bài 3. Phép cộng và phép trừ đa thức
Luyện tập chung trang 17
Bài 4. Phép nhân đa thức
Bài 5. Phép chia đa thức cho đơn thức
Luyện tập chung trang 25
Bài tập cuối chương 1
CHƯƠNG 2. HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG
Bài 6. Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Bài 7. Lập phương của một tổng. Lập phương của một hiệu
Bài 8. Tổng và hiệu hai lập phương
Luyện tập chung trang 40
Bài 9. Phân tích đa thức thành nhân tử
Luyện tập chung trang 45
Bài tập cuối chương 2
CHƯƠNG 3. TỨ GIÁC
Bài 10. Tứ giác
Bài 11. Hình thang cân
Luyện tập chung trang 56
Bài 12. Hình bình hành
Luyện tập chung trang 62
Bài 13. Hình chữ nhật
Bài 14. Hình thoi và hình vuông
Luyện tập chung trang 73
Bài tập cuối chương 3
CHƯƠNG 4. ĐỊNH LÍ THALES
Bài 15. Định lí Thales trong tam giác
Bài 16. Đường trung bình của tam giác
Bài 17. Tính chất đường phân giác của tam giác
Luyện tập chung trang 87
Bài tập cuối chương 4
CHƯƠNG 5. DỮ LIỆU VÀ BIỂU ĐỒ
Bài 18. Thu thập và phân loại dữ liệu
Bài 19. Biểu diễn dữ liệu bằng bảng, biểu đồ
Bài 20. Phân tích dữ liệu thống kê dựa vào biểu đồ
Luyện tập chung trang 106
Bài tập cuối chương 5
CHƯƠNG 6. PHÂN THỨC ĐẠI SỐ
Bài 21. Phân thức đại số
Bài 22. Tính chất cơ bản của phân thức đại số
Luyện tập chung trang 13
Bài 23. Phép cộng và phép trừ phân thức đại số
Bài 24. Phép nhân và phép chia phân thức đại số
Luyện tập chung trang 23
Bài tập cuối chương 6
CHƯƠNG 7. PHƯƠNG TRÌNH BẬC NHẤT VÀ HÀM SỐ BẬC NHẤT
Bài 25. Phương trình bậc nhất một ẩn
Bài 26. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 37
Bài 27. Khái niệm hàm số và đồ thị của hàm số
Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài 29. Hệ số góc của đường thẳng
Luyện tập chung trang 55
Bài tập cuối chương 7
CHƯƠNG 8. MỞ ĐẦU VỀ TÍNH XÁC SUẤT CỦA BIẾN CỐ
Bài 30. Kết quả có thể và kết quả thuận lợi
Bài 31. Cách tính xác suất của biến cố bằng tỉ số
Bài 32. Mối liên hệ giữa xác suất thực nghiệm với xác suất ứng dụng
Luyện tập chung trang 74
Bài tập cuối chương 8
CHƯƠNG 9. TAM GIÁC ĐỒNG DẠNG
Bài 33. Hai tam giác đồng dạng
Bài 34. Ba trường hợp đồng dạng của hai tam giác
Luyện tập chung trang 91
Bài 35. Định lí Pythagore và ứng dụng
Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
Bài 37. Hình đồng dạng
Luyện tập chung trang 108
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 38. Hình chóp tam giác đều
Bài 39. Hình chóp tứ giác đều
Luyện tập chung trang 121
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Công thức lãi kép
Thực hiện tính toán trên đa thức với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm GeoGebra
Phân tích đặc điểm khí hậu Việt Nam
Một vài ứng dụng của hàm số bậc nhất trong tài chính
Ứng dụng định lí Thalès, định lí Pythagore và tam giác đồng dạng để đo chiều cao, khoảng cách
Thực hành tính toán trên phân thức đại số và vẽ đồ thị hàm số với phần mềm GeoGebra
Mô tả thí nghiệm ngẫu nhiên với phần mềm Excel
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Trường hợp cạnh huyền cạnh góc vuông Toán 9 có đáp án
Trắc nghiệm Trường hợp cạnh huyền cạnh góc vuông
17 câu hỏi
30 phút
Trắc nghiệm
Câu 1 :
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\frac{{AB}}{{DE}} = \frac{{BC}}{{FE}}\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Câu 2 :
Hai tam giác vuông đồng dạng với nhau khi:
-
A.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt tỉ lệ với hai cạnh góc vuông của tam giác kia
-
B.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt nhỏ hơn với cạnh huyền và một cạnh góc vuông của tam giác kia
-
C.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia
-
D.
Cả A, B, C đều sai
-
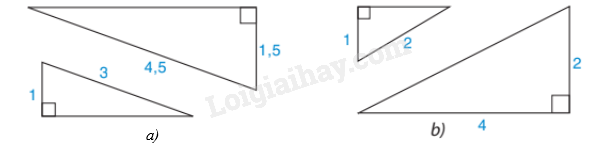
A.
Hình a thể hiện hai tam giác đồng dạng
-
B.
Hình b thể hiện hai tam giác đồng dạng
-
C.
Cả hình a, b đều thể hiện hai tam giác đồng dạng
-
D.
Cả hình a, b đều không thể hiện hai tam giác đồng dạng
Câu 4 :
Cho tam giác ABC vuông tại A có: \(AB = 3cm,BC = 5cm\) và tam giác MNP vuông tại M có \(MN = 6cm,NP = 10cm.\) Khi đó,
-
A.
\(\Delta ABC = \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta MNP\)
-
C.
\(\Delta BAC \backsim \Delta MNP\)
-
D.
\(\Delta BCA \backsim \Delta MNP\)
Câu 5 :
Cho hai tam giác vuông ABC và ADE có các kích thước như hình dưới. Khẳng định nào sau đây đúng?
-
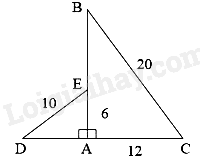
A.
\(\Delta ADE \backsim \Delta BAC\)
-
B.
\(\Delta ADE \backsim \Delta ABC\)
-
C.
\(\Delta ADE \backsim \Delta CBA\)
-
D.
Không có hai tam giác nào đồng dạng với nhau
Câu 6 :
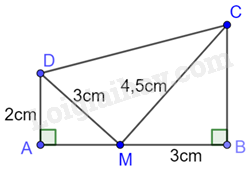
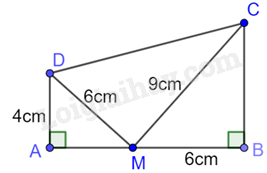
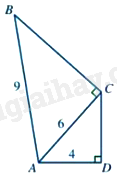
Cho tứ giác ABCD có \(AB = 9cm,\;AC = 6cm,AD = 4,\widehat {ADC} = \widehat {ACB} = {90^0}\) (như hình vẽ)
Khẳng định nào sau đây đúng?
-
A.
\(\widehat {BAC} = \widehat {CAD}\)
-
B.
\(\widehat {BAC} = \frac{2}{3}\widehat {CAD}\)
-
C.
\(\frac{2}{3}\widehat {BAC} = \widehat {CAD}\)
-
D.
\(\widehat {BAC} = \frac{3}{4}\widehat {CAD}\)
-
A.
\(\widehat {DMC} = {80^0}\)
-
B.
\(\widehat {DMC} = {90^0}\)
-
C.
\(\widehat {DMC} = {100^0}\)
-
D.
\(\widehat {DMC} = {70^0}\)
Câu 8 :
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\) Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Số đo góc ABD bằng bao nhiêu độ?
-
A.
80\(^0\).
-
B.
90\(^0\).
-
C.
95\(^0\).
-
D.
85\(^0\).
Câu 9 :
Tam giác ABH vuông tại H có \(AB = 20cm,BH = 12cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Khi đó, số đo góc BAC bằng:
-
A.
80\(^0\)
-
B.
90\(^0\)
-
C.
95\(^0\)
-
D.
85\(^0\)
Câu 10 :
Cho tam giác ABC cân tại A, đường cao AH và M là trọng tâm của tam giác ABC; tam giác A’B’C’ cân tại A’, đường cao A’H và M’ là trọng tâm tâm của tam giác A’B’C’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{AB}}{{A'B'}} = 3.\) Chọn đáp án đúng.
-
A.
\(\frac{{BM}}{{B'M'}} = \frac{7}{4}\)
-
B.
\(\frac{{BM}}{{B'M'}} = \frac{5}{2}\)
-
C.
\(\frac{{BM}}{{B'M'}} = \frac{3}{2}\)
-
D.
\(\frac{{BM}}{{B'M'}} = 3\)
Câu 11 :
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\)Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Diện tích tam giác ABD bằng:
-
A.
\(9\sqrt {20} c{m^2}\)
-
B.
\(\frac{9}{2}\sqrt {20} c{m^2}\)
-
C.
\(\sqrt {20} c{m^2}\)
-
D.
\(\frac{9}{4}\sqrt {20} c{m^2}\)
Câu 12 :
Tam giác ABH vuông tại H có \(AB = 25cm,BH = 15cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Chu vi tam giác AHC là:
-
A.
80cm
-
B.
90cm
-
C.
70cm
-
D.
100cm
-
A.
\(15 - \sqrt {117} cm\)
-
B.
\(15 + \sqrt {117} cm\)
-
C.
\(15 + \sqrt {118} cm\)
-
D.
\(15 - \sqrt {118} cm\)
Câu 14 :
Cho tam giác ABC cân tại A có chu vi bằng 60cm và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\). Chu vi tam giác A’B’C’ là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
40cm
Câu 15 :
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{CH}}{{C'H'}} = \frac{{BC}}{{B'C'}}\). Biết rằng \(\widehat {BAC} = 4\widehat {A'C'B'}.\) Chọn đáp án đúng.
-
A.
\(\widehat {BAC} = {90^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Câu 16 :
Cho điểm B nằm trên đoạn thẳng AC sao cho \(AB = 6cm,BC = 24cm.\) Vẽ về một phía của AC tia Ax và Cy vuông góc với AC. Trên tia Ax lấy điểm E sao cho \(EB = 10cm,\) trên tia Cy lấy điểm D sao cho \(BD = 30cm.\)
Cho các khẳng định sau:
1. Tam giác EBD là tam giác nhọn.
2. Diện tích tam giác EBD bằng \(150c{m^2}\).
3. Chu vi tam giác EBD bằng 60cm.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Câu 17 :
Cho hai hình chữ nhật ABCD và A’B’C’D’ thỏa mãn \(AC = 3AB,B'D' = 3A'B'\)
Nếu \(AB = 2A'B'\) và diện tích hình chữ nhật ABCD là \(12{m^2}\) thì diện tích hình chữ nhật A’B’C’D’ là bao nhiêu?
-
A.
\(6{m^2}\)
-
B.
\(8{m^2}\)
-
C.
\(10{m^2}\)
-
D.
\(3{m^2}\)
CÁC BÀI TẬP KHÁC
