Copyright © 2021 loigiaihay.com
CHƯƠNG 1. ĐA THỨC
Bài 1. Đơn thức
Bài 2. Đa thức
Bài 3. Phép cộng và phép trừ đa thức
Luyện tập chung trang 17
Bài 4. Phép nhân đa thức
Bài 5. Phép chia đa thức cho đơn thức
Luyện tập chung trang 25
Bài tập cuối chương 1
CHƯƠNG 2. HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG
Bài 6. Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Bài 7. Lập phương của một tổng. Lập phương của một hiệu
Bài 8. Tổng và hiệu hai lập phương
Luyện tập chung trang 40
Bài 9. Phân tích đa thức thành nhân tử
Luyện tập chung trang 45
Bài tập cuối chương 2
CHƯƠNG 3. TỨ GIÁC
Bài 10. Tứ giác
Bài 11. Hình thang cân
Luyện tập chung trang 56
Bài 12. Hình bình hành
Luyện tập chung trang 62
Bài 13. Hình chữ nhật
Bài 14. Hình thoi và hình vuông
Luyện tập chung trang 73
Bài tập cuối chương 3
CHƯƠNG 4. ĐỊNH LÍ THALES
Bài 15. Định lí Thales trong tam giác
Bài 16. Đường trung bình của tam giác
Bài 17. Tính chất đường phân giác của tam giác
Luyện tập chung trang 87
Bài tập cuối chương 4
CHƯƠNG 5. DỮ LIỆU VÀ BIỂU ĐỒ
Bài 18. Thu thập và phân loại dữ liệu
Bài 19. Biểu diễn dữ liệu bằng bảng, biểu đồ
Bài 20. Phân tích dữ liệu thống kê dựa vào biểu đồ
Luyện tập chung trang 106
Bài tập cuối chương 5
CHƯƠNG 6. PHÂN THỨC ĐẠI SỐ
Bài 21. Phân thức đại số
Bài 22. Tính chất cơ bản của phân thức đại số
Luyện tập chung trang 13
Bài 23. Phép cộng và phép trừ phân thức đại số
Bài 24. Phép nhân và phép chia phân thức đại số
Luyện tập chung trang 23
Bài tập cuối chương 6
CHƯƠNG 7. PHƯƠNG TRÌNH BẬC NHẤT VÀ HÀM SỐ BẬC NHẤT
Bài 25. Phương trình bậc nhất một ẩn
Bài 26. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 37
Bài 27. Khái niệm hàm số và đồ thị của hàm số
Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài 29. Hệ số góc của đường thẳng
Luyện tập chung trang 55
Bài tập cuối chương 7
CHƯƠNG 8. MỞ ĐẦU VỀ TÍNH XÁC SUẤT CỦA BIẾN CỐ
Bài 30. Kết quả có thể và kết quả thuận lợi
Bài 31. Cách tính xác suất của biến cố bằng tỉ số
Bài 32. Mối liên hệ giữa xác suất thực nghiệm với xác suất ứng dụng
Luyện tập chung trang 74
Bài tập cuối chương 8
CHƯƠNG 9. TAM GIÁC ĐỒNG DẠNG
Bài 33. Hai tam giác đồng dạng
Bài 34. Ba trường hợp đồng dạng của hai tam giác
Luyện tập chung trang 91
Bài 35. Định lí Pythagore và ứng dụng
Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
Bài 37. Hình đồng dạng
Luyện tập chung trang 108
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 38. Hình chóp tam giác đều
Bài 39. Hình chóp tứ giác đều
Luyện tập chung trang 121
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Công thức lãi kép
Thực hiện tính toán trên đa thức với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm GeoGebra
Phân tích đặc điểm khí hậu Việt Nam
Một vài ứng dụng của hàm số bậc nhất trong tài chính
Ứng dụng định lí Thalès, định lí Pythagore và tam giác đồng dạng để đo chiều cao, khoảng cách
Thực hành tính toán trên phân thức đại số và vẽ đồ thị hàm số với phần mềm GeoGebra
Mô tả thí nghiệm ngẫu nhiên với phần mềm Excel
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Trường hợp góc nhọn Toán 9 có đáp án
Trắc nghiệm Trường hợp góc nhọn
23 câu hỏi
30 phút
Trắc nghiệm
Câu 1 :
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\widehat B = \widehat F\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
-
A.
\(\Delta IPQ \backsim \Delta IMN\)
-
B.
\(\Delta IPQ = \Delta IMN\)
-
C.
\(\Delta IPQ \backsim \Delta INM\)
-
D.
\(\Delta IPQ \backsim \Delta MNI\)
Câu 3 :
Cho các mệnh đề sau. Chọn câu đúng.
(I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
(II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
-
A.
(I) đúng, (II) sai
-
B.
(I) sai, (II) đúng
-
C.
(I) và (II) đều sai
-
D.
(I) và (II) đều đúng
Câu 4 :
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(\Delta ACH \backsim \Delta BCA\)
-
B.
\(\Delta ACH \backsim \Delta CBA\)
-
C.
\(\Delta ACH \backsim \Delta BAC\)
-
D.
\(\Delta ACH \backsim \Delta CBA\)
-
A.
\(\frac{{BC}}{{BE}} = 2\frac{{BD}}{{BA}}\)
-
B.
\(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
C.
\(2\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)
-
D.
A, B, C đều sai
Câu 6 :
Một người ở vị trí điểm A muốn đo khoảng cách đến điểm B ở bên kia sông mà không thể qua sông được. Sử dụng giác kế, người đó xác định được một điểm M trên bờ sông sao cho \(AM = 2m,AM \bot AB\) và đo được góc AMB. Tiếp theo, người đó vẽ trên giấy tam giác A’M’B’ vuông tại A’ có \(A'M' = 1cm,\;\widehat {A'M'B'} = \widehat {AMB}\) và đo được \(A'B' = 5cm\) (hình vẽ dưới). Khoảng cách từ A đến B bằng:
-
A.
4m
-
B.
6m
-
C.
8m
-
D.
10m
-
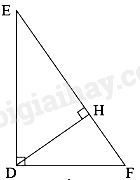
A.
\(D{H^2} = HE + 2HF\)
-
B.
\(D{H^2} = HE.HF\)
-
C.
\(D{H^2} = HE + HF\)
-
D.
\(D{H^2} = HE - HF\)
Câu 8 :
Cho tam giác ABC vuông tại A có \(\widehat B = {30^0}\), tam giác MNP vuông tại M có \(\widehat N = {60^{0.}}\)
Chọn đáp án đúng.
-
A.
\(AB.PN = MP.BC\)
-
B.
\(AB.MP = PN.BC\)
-
C.
\(AB.MP = 2PN.BC\)
-
D.
\(AB.PN = 2MP.BC\)
Câu 9 :
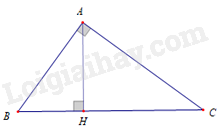
Cho tam giác ABC vuông tại A, đường cao AH. Khẳng định nào sau đây đúng?
-
A.
\(2AC = CH.BC\)
-
B.
\(A{C^2} = \frac{1}{2}CH.BC\)
-
C.
\(A{C^2} = CH.BC\)
-
D.
\(A{C^2} = 2CH.BC\)
Câu 10 :
Cho tam giác \(ABC\) cân tại \(A\) , đường cao \(CE\) . Tính \(AB\) , biết \(BC = 24\) cm và \(BE = 9\) cm.
-
A.
16cm
-
B.
32cm
-
C.
24cm
-
D.
18cm
-
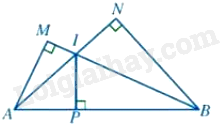
A.
\(AI.AN + BI.BM = 2A{B^2}\)
-
B.
\(AI.AN + BI.BM = A{B^2}\)
-
C.
\(AI.AN + 2BI.BM = A{B^2}\)
-
D.
\(2AI.AN + BI.BM = A{B^2}\)
-
A.
\(y = 10\)
-
B.
\(x = 4,8\)
-
C.
A, B đều đúng
-
D.
A, B đều sai
Câu 13 :
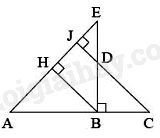
Cho tam giác ABC cân tại A, \(AC = 20cm,BC = 24cm.\) Các đường cao AD và CE cắt nhau tại H. Khi đó,
-
A.
\(HD = 12cm\)
-
B.
\(HD = 6cm\)
-
C.
\(HD = 9cm\)
-
D.
\(HD = 10cm\)
Câu 14 :
Cho tam giác ABC vuông tại A, đường cao AH chia đoạn BC thành hai đoạn thẳng \(HB = 7cm,HC = 18cm.\) Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác thành 2 phần có diện tích bằng nhau. Khi đó,
-
A.
\(CE = 15cm\)
-
B.
\(CE = 16cm\)
-
C.
\(CE = 12cm\)
-
D.
\(CE = 10cm\)
Câu 15 :
Cho hình bình hành ABCD \(\left( {AC > AB} \right)\) . Gọi E là hình chiếu của C trên AB, K là hình chiếu của C trên AD và H là hình chiếu của B trên AC.
Chọn đáp án đúng.
-
A.
\(AB.AE + AD.AK = 2A{C^2}\)
-
B.
\(2AB.AE + AD.AK = A{C^2}\)
-
C.
\(AB.AE + 2AD.AK = A{C^2}\)
-
D.
\(AB.AE + AD.AK = A{C^2}\)
Câu 16 :
Cho tam giác ABC vuông tại A. Lấy một điểm M bất kì trên cạnh AC. Từ C vẽ một đường thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. Khi đó:
-
A.
\(BM.BD + CM.CA = \frac{1}{2}B{C^2}\)
-
B.
\(BM.BD + 2CM.CA = B{C^2}\)
-
C.
\(BM.BD + CM.CA = B{C^2}\)
-
D.
\(BM.BD + CM.CA = 2B{C^2}\)
Câu 17 :
Cho tam giác ABC cân tại A, đường cao CE. Biết rằng \(BE = 3cm,BC = 8cm.\)
Độ dài đoạn thẳng AB là:
-
A.
\(\frac{{34}}{3}cm\)
-
B.
32cm
-
C.
\(\frac{{32}}{3}cm\)
-
D.
35cm
-
A.
\(\Delta ABC\,\backsim \Delta ABH\) .
-
B.
\(\Delta ABC\,\backsim \,\Delta HAB\) .
-
C.
\(\Delta ABC\,\backsim \,\Delta AHB\) .
-
D.
\(\Delta ABC\,\backsim \,\Delta HBA\) .
Câu 19 :
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Hệ thức nào sau đây đúng?
-
A.
\(AB = BC.BH\).
-
B.
\(A{C^2} = CH.BH\).
-
C.
\(A{H^2} = BH.CH\).
-
D.
\(AH = CH.BH\).
Câu 20 :
Cho hình thang vuông \(ABCD\), \(\left( {\widehat A = \widehat D = 90^\circ } \right)\) có \(DB \bot BC\), \(AB = 4\,{\rm{cm}}\), \(CD = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(BD\) là
-
A.
\(8\,{\rm{cm}}\).
-
B.
\(12\,{\rm{cm}}\).
-
C.
\(9\,{\rm{cm}}\).
-
D.
\(6\,{\rm{cm}}\).
Câu 21 :
Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\) biết \(BH = 4\,{\rm{cm}}\), \(CH = 9\,{\rm{cm}}\). Độ dài đoạn thẳng \(AH\) là
-
A.
\(4,8\,{\rm{cm}}\).
-
B.
\(5\,{\rm{cm}}\).
-
C.
\(6\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Câu 22 :
Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 30\,{\rm{cm}}\), \(AC = 40\,{\rm{cm}}\). Kẻ đường cao \(AH\)\(\left( {H \in BC} \right)\). Độ dài đường cao \(AH\) là
-
A.
\(18\,{\rm{cm}}\).
-
B.
\(24\,{\rm{cm}}\).
-
C.
\(32\,{\rm{cm}}\).
-
D.
\(36\,{\rm{cm}}\).
Câu 23 :
\(\Delta ABC\) cân tại \(A\), hai đường cao \(AH\) và \(BK\), cho \(BC = 6\,{\rm{cm}}\), \(AB = 5\,{\rm{cm}}\). Độ dài đoạn thẳng \(BK\) là
-
A.
\(4,5\,{\rm{cm}}\).
-
B.
\(4,8\,{\rm{cm}}\).
-
C.
\(3\,{\rm{cm}}\).
-
D.
\(4\,{\rm{cm}}\).
CÁC BÀI TẬP KHÁC
