Copyright © 2021 loigiaihay.com
CHƯƠNG 1. ĐA THỨC
Bài 1. Đơn thức
Bài 2. Đa thức
Bài 3. Phép cộng và phép trừ đa thức
Luyện tập chung trang 17
Bài 4. Phép nhân đa thức
Bài 5. Phép chia đa thức cho đơn thức
Luyện tập chung trang 25
Bài tập cuối chương 1
CHƯƠNG 2. HẰNG ĐẲNG THỨC ĐÁNG NHỚ VÀ ỨNG DỤNG
Bài 6. Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
Bài 7. Lập phương của một tổng. Lập phương của một hiệu
Bài 8. Tổng và hiệu hai lập phương
Luyện tập chung trang 40
Bài 9. Phân tích đa thức thành nhân tử
Luyện tập chung trang 45
Bài tập cuối chương 2
CHƯƠNG 3. TỨ GIÁC
Bài 10. Tứ giác
Bài 11. Hình thang cân
Luyện tập chung trang 56
Bài 12. Hình bình hành
Luyện tập chung trang 62
Bài 13. Hình chữ nhật
Bài 14. Hình thoi và hình vuông
Luyện tập chung trang 73
Bài tập cuối chương 3
CHƯƠNG 4. ĐỊNH LÍ THALES
Bài 15. Định lí Thales trong tam giác
Bài 16. Đường trung bình của tam giác
Bài 17. Tính chất đường phân giác của tam giác
Luyện tập chung trang 87
Bài tập cuối chương 4
CHƯƠNG 5. DỮ LIỆU VÀ BIỂU ĐỒ
Bài 18. Thu thập và phân loại dữ liệu
Bài 19. Biểu diễn dữ liệu bằng bảng, biểu đồ
Bài 20. Phân tích dữ liệu thống kê dựa vào biểu đồ
Luyện tập chung trang 106
Bài tập cuối chương 5
CHƯƠNG 6. PHÂN THỨC ĐẠI SỐ
Bài 21. Phân thức đại số
Bài 22. Tính chất cơ bản của phân thức đại số
Luyện tập chung trang 13
Bài 23. Phép cộng và phép trừ phân thức đại số
Bài 24. Phép nhân và phép chia phân thức đại số
Luyện tập chung trang 23
Bài tập cuối chương 6
CHƯƠNG 7. PHƯƠNG TRÌNH BẬC NHẤT VÀ HÀM SỐ BẬC NHẤT
Bài 25. Phương trình bậc nhất một ẩn
Bài 26. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 37
Bài 27. Khái niệm hàm số và đồ thị của hàm số
Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất
Bài 29. Hệ số góc của đường thẳng
Luyện tập chung trang 55
Bài tập cuối chương 7
CHƯƠNG 8. MỞ ĐẦU VỀ TÍNH XÁC SUẤT CỦA BIẾN CỐ
Bài 30. Kết quả có thể và kết quả thuận lợi
Bài 31. Cách tính xác suất của biến cố bằng tỉ số
Bài 32. Mối liên hệ giữa xác suất thực nghiệm với xác suất ứng dụng
Luyện tập chung trang 74
Bài tập cuối chương 8
CHƯƠNG 9. TAM GIÁC ĐỒNG DẠNG
Bài 33. Hai tam giác đồng dạng
Bài 34. Ba trường hợp đồng dạng của hai tam giác
Luyện tập chung trang 91
Bài 35. Định lí Pythagore và ứng dụng
Bài 36. Các trường hợp đồng dạng của hai tam giác vuông
Bài 37. Hình đồng dạng
Luyện tập chung trang 108
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 38. Hình chóp tam giác đều
Bài 39. Hình chóp tứ giác đều
Luyện tập chung trang 121
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Công thức lãi kép
Thực hiện tính toán trên đa thức với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm GeoGebra
Phân tích đặc điểm khí hậu Việt Nam
Một vài ứng dụng của hàm số bậc nhất trong tài chính
Ứng dụng định lí Thalès, định lí Pythagore và tam giác đồng dạng để đo chiều cao, khoảng cách
Thực hành tính toán trên phân thức đại số và vẽ đồ thị hàm số với phần mềm GeoGebra
Mô tả thí nghiệm ngẫu nhiên với phần mềm Excel
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Diện tích xung quanh và thể tích hình chóp tam giác Toán 9 có đáp án
Trắc nghiệm Diện tích xung quanh và thể tích hình chóp tam giác
13 câu hỏi
30 phút
Trắc nghiệm
Câu 1 :
Diện tích toàn phần của hình chóp tam giác đều được tính bằng?
-
A.
tổng diện tích các mặt bên.
-
B.
diện tích mặt đáy.
-
C.
tổng diện tích xung quanh và diện tích đáy.
-
D.
hiệu của diện tích xung quanh và diện tích đáy.
Câu 2 :
Cho hình chóp tam giác đều có diện tích một mặt bên là S. Công thức tính diện tích xung quanh của hình chóp tam giác đều bằng:
-
A.
\({S_{xq}} = \frac{S}{4}\).
-
B.
\({S_{xq}} = \frac{S}{3}\).
-
C.
\({S_{xq}} = 4.S\).
-
D.
. \({S_{xq}} = 3.S\).
Câu 3 :
Cho hình chóp tam giác đều có thể tích V, chiều cao h. Công thức tính diện tích mặt đáy S của hình chóp là:
-
A.
\(S = \frac{V}{h}\)
-
B.
\(S = \frac{{3V}}{h}\)
-
C.
\(S = \frac{V}{{3h}}\)
-
D.
\(S = 3V.h\)
Câu 4 :
Cho hình chóp tam giác đều có diện tích một mặt bên là \(50c{m^2}\).Tính diện tích xung quanh của hình chóp đó.
-
A.
\(50c{m^2}\).
-
B.
\(\frac{{100}}{3}c{m^2}\)
-
C.
\(150c{m^2}\).
-
D.
\(100c{m^2}\).
Câu 5 :
Cho hình chóp tam giác đều có thể tích là \(250c{m^3}\), chiều cao hình chóp bằng \(30cm\). Tính diện tích mặt đáy của hình chóp đó.
-
A.
\(7500c{m^2}\).
-
B.
\(25c{m^2}\)
-
C.
\(250c{m^2}\).
-
D.
\(\frac{{25}}{3}c{m^2}\).
Câu 6 :
Cho hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của hình chóp là \(9cm\). Tính thể tích của hình chóp đó.
-
A.
\(48c{m^3}\).
-
B.
\(144c{m^3}\)
-
C.
\(72c{m^3}\).
-
D.
\(36c{m^3}\).
Câu 7 :
Cho hình chóp tam giác đều S.ABC có các mặt bên là các tam giác cân diện tích \(10c{m^2}\), diện tích mặt đáy là \(20c{m^2}\). Tính diện tích toàn phần của hình chóp đó.
-
A.
\(50c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(30c{m^2}\).
Câu 8 :
Tính diện tích bìa cần để làm một hộp quà hình chóp tam giác đều có bốn mặt là tam giác đều bằng nhau cạnh 4,4cm và chiều cao mặt đáy bằng 3cm ( không tính mép dán)
-
A.
\(24,6c{m^2}\)
-
B.
\(20c{m^2}\)
-
C.
\(40c{m^2}\)
-
D.
\(26,4c{m^2}\).
Câu 9 :
. Một chiếc bánh hình chóp tam giác đều có chiều cao của hình chóp là \(9cm\), tam giác đáy có cạnh đáy bằng 4cm , chiều cao bằng \(2\sqrt 2 cm\).Tính thể tích của chiếc bánh đó.
-
A.
\(12c{m^3}\).
-
B.
\(24c{m^3}\)
-
C.
\(12\sqrt 2 c{m^3}\).
-
D.
\(24\sqrt 2 c{m^3}\).
Câu 10 :
Cho hình chóp tam giác đều có thể tích là \(250c{m^2}\), diện tích đáy bằng\(50c{m^2}\). Tính chiều cao của hình chóp đó.
-
A.
\(15cm\).
-
B.
\(5cm\)
-
C.
\(10cm\).
-
D.
\(25cm\).
Câu 11 :
Cho hình chóp tam giác đều nằm trong một lăng trụ đứng đáy là tam giác đều như hình, Biết diện tích xung quanh của lăng trụ đứng bằng \(36c{m^2}\), chiều cao mặt đáy bằng \(2\sqrt 3 cm\), cạnh đáy bằng 4cm. Tính thể tích hình chóp tam giác đều.
-
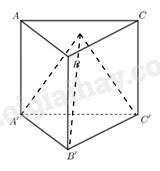
A.
\(4c{m^3}\).
-
B.
\(4\sqrt 3 c{m^3}\).
-
C.
\(8\sqrt 3 c{m^3}\).
-
D.
\(8c{m^3}\).
Câu 12 :
Cho hình chóp tam giác đều S.ABC có chu vi đáy bằng 9cm, chiều cao mặt đáy bằng \(\frac{{3\sqrt 3 }}{2}cm\), chiều cao hình chóp bằng \(\frac{3}{2}\)độ dài cạnh đáy. Thể tích V của khối chóp S.ABC.
-
A.
\(\frac{{81\sqrt 3 }}{4}c{m^3}\).
-
B.
\(\frac{{27\sqrt 3 }}{8}c{m^3}\).
-
C.
\(\frac{{81\sqrt 3 }}{8}c{m^3}\).
-
D.
\(\frac{{27\sqrt 3 }}{4}c{m^3}\).
Câu 13 :
Một người định làm một chiếc đèn trang trí dạng hình chóp tam giác đều. Chu vi mặt đáy bằng 90cm, chiều cao một mặt bên bằng 60cm. Người ta sẽ dán các mặt xung quanh đèn bằng giấy màu. Tính số tiền người người đó mua giấy màu để dán đèn, biết \(1{m^2}\) có giá 120000 đồng.
-
A.
32400 đồng.
-
B.
324000 đồng.
-
C.
3240 đồng.
-
D.
3240000 đồng.
CÁC BÀI TẬP KHÁC
