Đề bài
Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu sai.
-
A.
BH // CD
-
B.
CH // BD
-
C.
BH = CD
-
D.
HB = HC
Phương pháp giải
Chứng minh tứ giác BHCD có BH // CD và HC // BD nên BHCD là hình bình hành, khi đó ta có các cặp cạnh tương ứng bằng nhau.
Lời giải của GV Loigiaihay.com
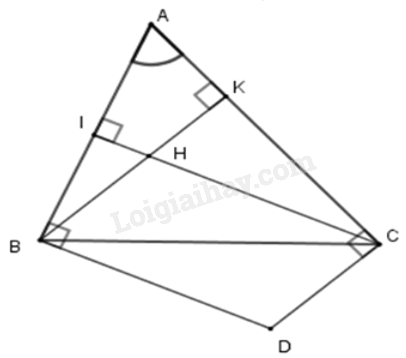
Gọi BK, CI là các đường cao của tam giác ABC. Khi đó BK ⊥ AC; CI ⊥ AB hay BH ⊥ AC; CH ⊥ AB (vì H là trực tâm).
Lại có BD ⊥ AB; CD ⊥ AC (giả thiết) nên BD // CH (cùng vuông với AB) và CD // BH (cùng vuông với AC)
Suy ra tứ giác BHCD là hình bình hành (dhnb)
Từ đó HB = CD; CH = BD nên D sai (ta chưa đủ điều kiện để chỉ ra được HB = HC)
Đáp án : D
