Bài 9 trang 92 Vở bài tập Toán 9 tập 2

Đề bài

a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.

Mệnh đề đảo có đúng không ? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.

Lời giải chi tiết

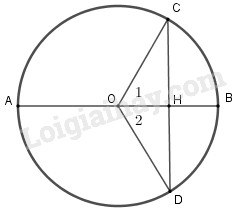
Giả sử đường kính \(AB\) cắt dây \(CD\) tại \(H.\) Nối \(O\) với \(C\) và \(D.\)

Từ giả thiết \(\overparen{CB}=\overparen{BD}\) 

nên \(\widehat {{O_1}} = \widehat {{O_2}}\) (hai góc ở tâm chắn hai cung bằng nhau thì bằng nhau) 

\( \Rightarrow AB\) (hay \(OH\)) là tia phân giác của tam giác cân \(OCD.\)

Vậy ta có \(HC = HD\) (đpcm).

Mệnh đề đảo : Giả sử \(HC = HD \Rightarrow \) \(\overparen{CB}=\overparen{BD}\) 

Xét trường hợp \(CD\) không đi qua tâm. Khi đó, \(\Delta OCD\) là tam giác cân vì \(OC = OD.\) Do đó, \(OH\) vừa là đường cao và là đường phân giác.

\( \Rightarrow \widehat {{O_1}} = \widehat {{O_2}}.\) Vậy theo tính chất góc ở tâm ta có \(\overparen{CB}=\overparen{BD}\) 

Khi \(CD\) đi qua tâm thì mệnh đề đảo sai.

Vậy để mệnh đề đảo đúng phải thêm điều kiện là dây cung không phải là đường kính.

b) Giả sử đường kính \(AB\) và \(\overparen{CB}=\overparen{BD}\)

Theo chứng minh câu a) ta có \(OH\) là tia phân giác của \(\Delta OCD\) và \(H\) thuộc đường thẳng \(AB\) nên \(AB \bot CD.\)

Ngược lại từ\(AB \bot CD\), xét \(\Delta OCD\) cân tại \(O.\) Vì \(H\) thuộc \(AB\) nên \(OH\) là đường cao đồng thời là đường phân giác. Suy ra \(\widehat {{O_1}} = \widehat {{O_2}}\).

Vậy theo tính chất về góc ở tâm ta có  \(\overparen{CB}=\overparen{BD}\) hay \(B\) là điểm chính giữa cung CD (đpcm). 

Loigiaihay.com