-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương 1 - Phép nhân và chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng, hình chóp đều
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 36 trang 97 Vở bài tập toán 8 tập 2
Giải bài 36 trang 97 VBT toán 8 tập 2. Bóng của một cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó,...
Đề bài
Bóng của một cột điện trên mặt đất có độ dài là \(4,5m\). Cùng thời điểm đó, một thanh sắt cao \(2,1m\) cắm vuông góc với mặt đất có bóng dài \(0,6m\). Tính chiều cao của cột điện.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất hai tam giác đồng dạng.
Lời giải chi tiết
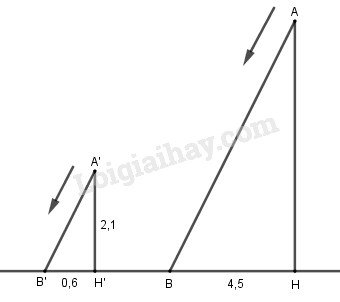
Gọi chiều cao của cột điện là \(AH\), bóng dài của cột điện là \(HB\) thì phương chiếu của tia nắng xuống mặt đất là \(AB\) (h.43).
Gọi chiều cao của thanh sắt \(A'H'\), bóng dài của thanh sắt \(H'B'\) thì phương chiếu của tia nắng xuống mặt đất là \(A'B'\).
Xét hai tam giác \(ABH\) và \(A'B'H'\):
Vì cột điện và thanh sắt cùng vuông góc với mặt đất, do đó: \(\Delta AHB\) và \(\Delta A'H'B'\) là hai tam giác vuông (\(AH \bot HB\);\(A'H' \bot H'B'\)).
Vì góc hợp bởi tia nắng và mặt đất như nhau, nên ta có:
\(\widehat {ABH} = \widehat {A'B'H'}\)
Suy ra \(\Delta ABH \backsim \Delta A'B'H'\)
Do đó \(\dfrac{{AH}}{{A'H'}} = \dfrac{{BH}}{{B'H'}}\) hay \(\dfrac{{AH}}{{2,1}} = \dfrac{{4,5}}{{0,6}}\)
Suy ra \(AH = \dfrac{{2,1.4,5}}{{0,6}} = 15,75\left( m \right)\)
Đáp số: Cột điện cao \(15,75m.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 37 trang 98 Vở bài tập toán 8 tập 2
- Bài 38 trang 98 Vở bài tập toán 8 tập 2
- Bài 39 trang 99 Vở bài tập toán 8 tập 2
- Bài 40 trang 100 Vở bài tập toán 8 tập 2
- Bài 35 trang 97 Vở bài tập toán 8 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
