Bài 4. Tính chất ba đường trung tuyến của tam giác

Bài 26 trang 78 Vở bài tập toán 7 tập 2


Giải bài 26 trang 78 VBT toán 7 tập 2. Cho tam giác DEF cân tại D với đường trung tuyến DI. a) Chứng minh ∆DEI = ∆DFI; b) Các góc DIE và góc DIF là những góc gì ?...

Đề bài

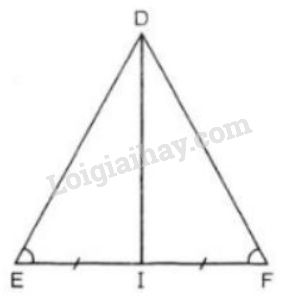
Cho tam giác \(DEF\) cân tại \(D\) với đường trung tuyến \(DI\). (h.25).

a) Chứng minh \(∆DEI  = ∆DFI;\)

b) Các góc \(DIE\) và góc \(DIF\) là những góc gì?

c) Biết \(DE = DF = 13\,cm,\) \(EF = 10\,cm,\) hãy tính độ dài đường trung tuyến \(DI.\) 

Phương pháp giải - Xem chi tiết

Áp dụng tính chất của tam giác cân, tính chất đường trung tuyến và định lý Pytago.

Lời giải chi tiết

a) Xét hai tam giác \(DEI\) và \(DFI\). 

Theo giả thiết ta có \(DE = DF\) và \(IE = IF\). Hơn nữa, \(DI\) là cạnh chung. Vậy \(∆DEI  = ∆DFI\) (c.c.c).

b) Theo câu a, \(∆DEI  = ∆DFI\), suy ra \(\widehat{DIE} =\widehat{DIF}\). Mặt khác, \(\widehat{DIE} +\widehat{DIF} = 180^o\), do đó \(\widehat{DIE} =\widehat{DIF}= 90^o\) 

c) Ta có tam giác \(DEI\) vuông tại \(I\) (câu b). Theo định lí Pytago, ta có \(DI = \sqrt {D{E^2} - E{I^2}} \)

Mặt khác, vì \(I\) là trung điểm của \( EF\) nên \(IE = IF =\dfrac{{EF}}{2} = \dfrac{{10}}{2}= 5\,(cm).\)

Vậy \(DI = \sqrt {{{13}^2} - {5^2}}  = 12\left( {cm} \right).\)

Loigiaihay.com


Bình chọn:
4.6 trên 25 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store