Bài 4. Tính chất ba đường trung tuyến của tam giác

Bài 24 trang 77 Vở bài tập toán 7 tập 2

Giải bài 24 trang 77 VBT toán 7 tập 2. Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau...

Đề bài

Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Phương pháp giải - Xem chi tiết

Áp dụng tính chất tam giác cân và trung tuyến của tam giác, từ đó chứng minh hai tam giác bằng nhau.

Lời giải chi tiết

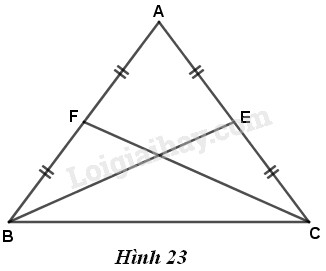
Xét hai tam giác \(ABE\) và \(ACF\).

Ta có: \(AB = AC\) (gt), góc \(A\) chung,

\(AE = \dfrac{{AC}}{2} = \dfrac{{AB}}{2} = AF\)

Vậy \(ΔABE = ΔACF\) (c.g.c), suy ra \(BE = CF\) (cặp cạnh tương ứng).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 15 phiếu

Bài 25 trang 77 Vở bài tập toán 7 tập 2
Giải bài 25 trang 77 VBT toán 7 tập 2. Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân...
Bài 26 trang 78 Vở bài tập toán 7 tập 2
Giải bài 26 trang 78 VBT toán 7 tập 2. Cho tam giác DEF cân tại D với đường trung tuyến DI. a) Chứng minh ∆DEI = ∆DFI; b) Các góc DIE và góc DIF là những góc gì ?...
Bài 27 trang 78 Vở bài tập toán 7 tập 2
Giải bài 27 trang 78 VBT toán 7 tập 2. Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng GA = GB = GC...
Bài 28 trang 79 Vở bài tập toán 7 tập 2
Giải bài 28 trang 79 VBT toán 7 tập 2. Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G’ sao cho G là trung điểm của AG’. a) So sánh các cạnh...
Bài 23 trang 76 Vở bài tập toán 7 tập 2
Giải bài 23 trang 76 VBT toán 7 tập 2. Biết rằng: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau...
Phần câu hỏi bài 4 trang 76 Vở bài tập toán 7 tập 2
Giải phần câu hỏi bài 4 trang 76 VBT toán 7 tập 2. Cho tam giác ABC với đường trung tuyến AM. Gọi G là trọng tâm của tam giác đó. Khoanh tròn vào chữ cái trước khẳng định đúng...