Bài 4. Vị trí tương đối của đường thẳng và đường tròn

Bài 15 trang 120 Vở bài tập toán 9 tập 1

Giải bài 15 trang 120 VBT toán 9 tập 1. Cho đường thẳng xy. Tâm của các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào ?

Đề bài

Cho đường thẳng \(xy\). Tâm của các đường tròn có bán kính \(1cm\) và tiếp xúc với đường thẳng \(xy\) nằm trên đường nào?

Phương pháp giải - Xem chi tiết

Vận dụng kiến thức : Đường thẳng a và đường tròn (O ; R). Gọi d là khoảng cách từ O đến a thì a tiếp xúc với (O) \( \Leftrightarrow d = R\).

Lời giải chi tiết

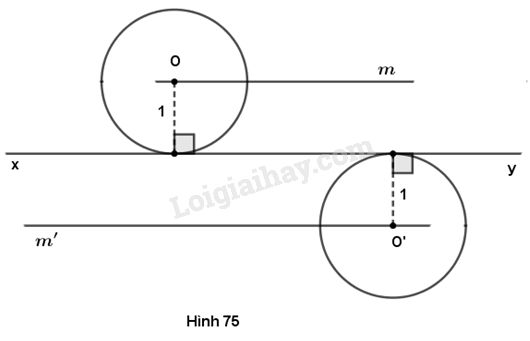
Gọi \(O\) là tâm của một đường tròn bất kì có bán kính \(1cm\) và tiếp xúc với đường thẳng \(xy.\) Gọi \(d\) là khoảng cách từ \(O\) đến \(xy.\) Đường tròn \( \left( {O;1cm} \right)\) tiếp xúc với đường thẳng \(xy\) nên \(d = R = 1cm.\)

Tâm \(O\) cách đường thẳng \(xy\) cố định \(1cm\) nên nằm trên hai đường thẳng \(m\) và \(m'\) song song với \(xy\) và cách \(xy\) một khoảng \(1cm.\)

Loigiaihay.com

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Các bài liên quan: - Bài 4. Vị trí tương đối của đường thẳng và đường tròn

Luyện Bài tập trắc nghiệm môn Toán lớp 9 - Xem ngay

Báo lỗi - Góp ý

>> Học trực tuyến lớp 9, luyện vào lớp 10, mọi lúc, mọi nơi môn Toán, Văn, Anh, Lý, Hóa, Sinh, Sử, Địa cùng các Thầy, Cô giáo giỏi nổi tiếng, dạy hay, dễ hiểu, dày dặn kinh nghiệm tại Tuyensinh247.com