Bài 3. Tính chất đường phân giác của tam giác

Bài 13 trang 77 Vở bài tập toán 8 tập 2

Giải bài 13 trang 77 VBT toán 8 tập 2. Cho hình thang ABCD (AB // CD) ...

Đề bài

Cho hình thang \(ABCD\) (\(AB // CD\)).

Đường thẳng \(a\) song song với \(DC\), cắt các cạnh \(AD\) và \(BC\) theo thứ tự là \(E\) và \(F.\)

Chứng minh rằng:

a) \(\dfrac{AE}{ED} = \dfrac{BF}{FC}\);

b) \(\dfrac{AE}{AD} = \dfrac{BF}{BC}\)

c) \(\dfrac{DE}{DA} = \dfrac{CF}{CB}\).

Phương pháp giải - Xem chi tiết

- Áp dụng tính chất của dãy tỉ số bằng nhau, định lí TaLet.

Lời giải chi tiết

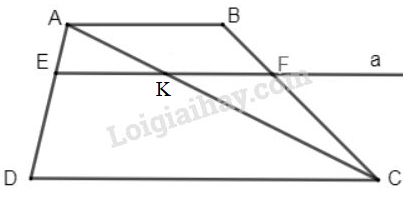
Vẽ thêm đường chéo \(AC\), \(AC\) cắt \(EF\) tại \(K\) (h.20)

+ Xét \(∆ACD\) có \(EK // DC\) (giả thiết)

Ta có: \( \dfrac{AE}{ED} = \dfrac{AK}{KC}\) (1)

+ Xét \(∆CAB\) có \(FK // AB\) (giả thiết)

Ta có: \(\dfrac{AK}{KC} = \dfrac{BF}{FC}\) (2)

Từ các tỉ lệ thức (1) và (2), ta suy ra: \( \dfrac{AE}{ED} = \dfrac{BF}{FC}\).

Tương tự như trên, xét \(\Delta ACD\) có \(EK//CD\) và \(\Delta CAB\) có \(KF//AB.\) Ta có:

\(\dfrac{{AE}}{{AD}} = \dfrac{{AK}}{{AC}};\,\dfrac{{AK}}{{AC}} = \dfrac{{BF}}{{BC}}.\) Suy ra \(\dfrac{{AE}}{{AD}} = \dfrac{{BF}}{{BC}}\).

\(\dfrac{{DE}}{{DA}} = \dfrac{{CK}}{{CA}};\,\dfrac{{CK}}{{CA}} = \dfrac{{CF}}{{CB}}.\) Suy ra \(\dfrac{{DE}}{{DA}} = \dfrac{{CF}}{{CB}}.\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài 14 trang 78 Vở bài tập toán 8 tập 2
Giải bài 14 trang 78 VBT toán 8 tập 2. Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O ...
Bài 15 trang 78 Vở bài tập toán 8 tập 2
Giải bài 15 trang 78 VBT toán 8 tập 2. Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM, biết AB= m, AC= n( n>m) và diện tích của tam giác ABC là S.
Bài 12 trang 76 Vở bài tập toán 8 tập 2
Giải bài 12 trang 76 VBT toán 8 tập 2. Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E.
Bài 11 trang 75 Vở bài tập toán 8 tập 2
Giải bài 11 trang 75 VBT toán 8 tập 2. Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng m/n
Phần câu hỏi bài 3 trang 75 Vở bài tập toán 8 tập 2
Giải phần câu hỏi bài 3 trang 75 VBT toán 8 tập 2. Cho biết O1 =O2 = O3 = O4. Hãy nhìn vào hình 16 rồi điền các tỉ số đúng vào những chỗ trống sau ...