Câu 25 trang 55 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp tứ giác S.ABCD có đáy là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của cạnh bên SA, SB, SC và SD.
Đề bài
Cho hình chóp tứ giác S.ABCD có đáy là một tứ giác lồi. Gọi M, N, E, F lần lượt là trung điểm của cạnh bên SA, SB, SC và SD. Chứng minh rằng:
a) ME//AC, NF//BD.
b) Ba đường thẳng ME, NF và SO (O là giao điểm của AC và BD) đồng quy.
c) Bốn điểm M, N, E, F đồng phẳng.
Lời giải chi tiết
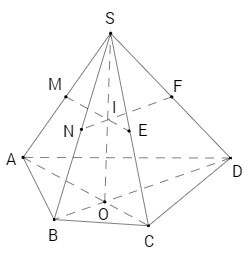
a) Xét tam gác SAC. Ta có ME là đường trung bình nên ME//AC. Lí luận tương tự, NF//BD.
b) Trong mp(SAC) gọi I là giao điểm của ME và SO. Dễ thấy I là trung điểm của SO. Từ đó FI là đường trung bình của tam giác SOD. Vậy FI//DO.
Gọi N’ là giao điểm của đường thẳng FI với SB.
Do FN' // BD và F là trung điểm của SD suy ra N’ là trung điểm của SB, tức là \(N' \equiv N.\)
Vậy ba đường thẳng ME, NF, SO đồng quy tại I.
c) Do ME và NF cắt nhau tại I, nên qua ME và NF xác định một mặt phẳng. Từ đó suy ra bốn điểm M, N, E, F đồng phẳng.
Loigiaihay.com
Các bài khác cùng chuyên mục













Danh sách bình luận