Giải SBT toán hình học và đại số 11 nâng cao Ôn tập chương II - Đường thẳng và mặt phẳng trong không..

Bài 68 trang 63 SBT Hình học 11 nâng cao.


Chứng minh rằng nếu n đường thẳng đôi một cắt nhau và không đồng phẳng thì chúng đồng quy.

Đề bài

Chứng minh rằng nếu n đường thẳng \(\left( {n \ge 3} \right)\) đôi một cắt nhau và không đồng phẳng thì chúng đồng quy.

Lời giải chi tiết

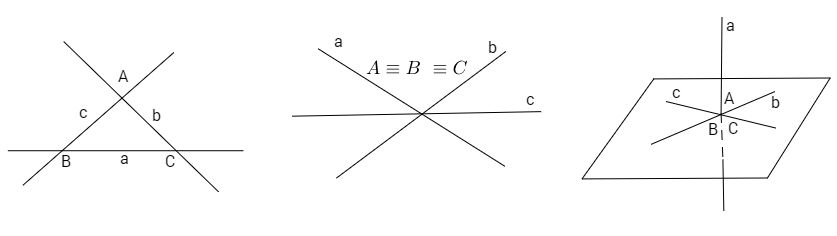
Ta nhận thấy rằng: Nếu ba đường thẳng bất kì trong n đường thẳng \(\left( {n \ge 3} \right)\)   đã cho đồng quy thì n đường thẳng đó đồng quy. Còn nếu tồn tại ba đường thẳng không đồng quy mà từng đôi một cắt nhau tại ba điểm A, B, C rõ ràng A, B, C không thẳng hàng. Khi đó các đường thẳng còn lại đều cắt ba đường thẳng nói trên nên chúng đều thuộc mp(ABC) (trái với giả thiết). Vậy ta chỉ cần chứng minh cho trường hợp n = 3.

Giả sử ba đường thẳng đã cho là a, b và c; A, B, C lần lượt là giao điểm của các cặp đường thẳng b và c, c và a, a và b. Nếu các điểm A, B, C phân biệt từng cặp thì dễ thấy a, b, c đều thuộc mp(ABC) (trái với giả thiết. Vậy các điểm A, B, C phải trùng nhau. Do đó ba đường thẳng a, b, c đồng quy.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua