Giải bài 3 trang 77 SGK Giải tích 12
Tìm tập xác định của các hàm số:
Video hướng dẫn giải
Tìm tập xác định của các hàm số:
LG a
a) \(y = {\log_2}\left( {5 - 2x} \right)\) ;
Phương pháp giải:
Hàm số \(y = {\log _a}{f \left( x \right)} \,\,\left( {0 < a \ne 1} \right)\) xác định khi và chỉ khi \(f \left( x \right) > 0\).
Lời giải chi tiết:
Hàm số \(y = {\log_2}\left( {5 - 2x} \right)\) xác định khi và chỉ khi:
\(5- 2x > 0\Leftrightarrow x < \dfrac{5}{2}.\)
Vậy hàm số \(y ={\log_2}\left( {5 - 2x} \right)\) có tập xác định là \(D=\left( \displaystyle{ - \infty ;{5 \over 2}} \right).\)
LG b
b) \(y ={\log_3}({x^2} - 2x)\) ;
Phương pháp giải:
Hàm số \(y = {\log _a}{f \left( x \right)} \,\,\left( {0 < a \ne 1} \right)\) xác định khi và chỉ khi \(f \left( x \right) > 0\).
Lời giải chi tiết:
Hàm số \(y ={\log_3}({x^2} - 2x)\) xác định khi và chỉ khi:
\({x^2} - 2x > 0 \Leftrightarrow \left[ \begin{array}{l}
x > 2\\
x < 0
\end{array} \right.\)
Vậy hàm số \(y ={\log_3}({x^2} - 2x)\) có tập xác định là \(D=(-∞; 0) ∪ (2;+∞)\).
LG c
c) \(y=\log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\);
Phương pháp giải:
Hàm số \(y = {\log _a}{f \left( x \right)} \,\,\left( {0 < a \ne 1} \right)\) xác định khi và chỉ khi \(f \left( x \right) > 0\).
Lời giải chi tiết:
Hàm số \(y=\log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\) xác định khi và chỉ khi
\({x^2} - 4x + 3 > 0 \Leftrightarrow \left[ \begin{array}{l}
x > 3\\
x < 1
\end{array} \right.\)
Vậy hàm số \(y= \log_{\frac{1}{5}}\left ( x^{2} -4x+3 \right )\) có tập xác định là \(D=(-∞; 1) ∪ (3;+∞)\).
LG d
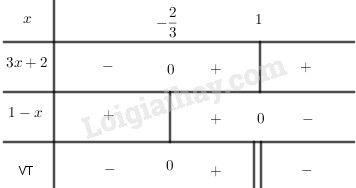
d) \(y= \log_{0,4}\dfrac{3x+2}{1-x}\).
Phương pháp giải:
Hàm số \(y = {\log _a}{f \left( x \right)} \,\,\left( {0 < a \ne 1} \right)\) xác định khi và chỉ khi \(f \left( x \right) > 0\).
Lời giải chi tiết:
Hàm số \(y= \log_{0,4}\dfrac{3x+2}{1-x}\) xác định khi và chỉ khi:
\(\dfrac{3x+2}{1-x} > 0\)
\(\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
3x + 2 > 0\\
1 - x > 0
\end{array} \right.\\
\left\{ \begin{array}{l}
3x + 2 < 0\\
1 - x < 0
\end{array} \right.
\end{array} \right. \)\(\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x > - \frac{2}{3}\\
x < 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x < - \frac{2}{3}\\
x > 1
\end{array} \right.\left( {VN} \right)
\end{array} \right. \)\(\Leftrightarrow - \frac{2}{3} < x < 1\)
Vậy hàm số \(y = \log_{0,4}\dfrac{3x+1}{1-x}\) có tập xác định là \(D=\left( \displaystyle{ - {2 \over 3};1} \right)\).
Chú ý:
Các em cũng có thể lập bảng xét dấu các nhị thức bậc nhất như sau:
Loigiaihay.com













Danh sách bình luận