Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn
Bài 2. Giải hệ hai phương trình bậc nhất hai ẩn
Luyện tập chung trang 19
Bài 3. Giải bài toán bằng cách lập hệ phương trình
Bài tập cuối chương 1
CHƯƠNG 2. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 4. Phương trình quy về phương trình bậc nhất một ẩn
Bài 5. Bất đẳng thức và tính chất
Luyện tập chung trang 36
Bài 6. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN BẬC HAI VÀ CĂN BẬC BA
Bài 7. Căn bậc hai và căn thức bậc hai
Bài 8. Khai căn bậc hai với phép nhân và phép chia
Luyện tập chung trang 52
Bài 9. Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai
Bài 10. Căn bậc ba và căn thức bậc ba
Luyện tập chung trang 63
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 11. Tỉ số lượng giác của góc nhọn
Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Luyện tập chung trang 79
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 13. Mở đầu về đường tròn
Bài 14. Cung và dây của một đường tròn
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
Luyện tập chung trang 96
Bài 16. Vị trí tương đối của đường thẳng và đường tròn
Bài 17. Vị trí tương đối của hai đường tròn
Luyện tập chung trang 108
Bài tập cuối chương 5
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 18. Hàm số y = ax^2 (a khác 0)
Bài 19. Phương trình bậc hai một ẩn
Luyện tập chung trang 18
Bài 20. Định lí Viète và ứng dụng
Bài 21. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 28
Bài tập cuối chương 6
CHƯƠNG 7. TẦN SỐ VÀ TẦN SỐ TƯƠNG ĐỐI
Bài 22. Bảng tần số và biểu đồ tần số
Bài 23. Bảng tần số tương đối và biểu đồ tần số tương đối
Luyện tập chung trang 43
Bài 24. Bảng tần số, tần số tương đối ghép nhóm và biểu đồ
Bài tập cuối chương 7
CHƯƠNG 8. XÁC SUẤT CỦA BIẾN CỐ TRONG MỘT SỐ MÔ HÌNH XÁC SUẤT ĐƠN GIẢN
Bài 25. Phép thử ngẫu nhiên và không gian mẫu
Bài 26. Xác suất của biến cố liên quan tới phép thử
Luyện tập chung trang 64
Bài tập cuối chương 8
CHƯƠNG 9. ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP
Bài 27. Góc nội tiếp
Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác
Luyện tập chung trang 78
Bài 29. Tứ giác nội tiếp
Bài 30. Đa giác đều
Luyện tập chung trang 90
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 31. Hình trụ và hình nón
Bài 32. Hình cầu
Luyện tập chung trang 106
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Pha chế dung dịch theo nồng độ yêu cầu
Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm Geogebra
Xác định tần số, tần số tương đối, vẽ các biểu đồ biểu diễn bảng tần số, tần số tương đối bằng Excel
Gene trội trong các thế hệ lai
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn Toán 9 có đáp án
Trắc nghiệm Tìm nghiệm tổng quát và vẽ đường thẳng biểu diễn
13 câu hỏi
Trắc nghiệm
Câu 1 :
Cho phương trình $ax + by = c$ với $a \ne 0,b \ne 0$. Nghiệm của phương trình được biểu diễn bởi
-
A.
$x \in R;y = - \dfrac{a}{b}x + \dfrac{c}{b}$
-
B.
$x \in R;y = - \dfrac{a}{b}x - \dfrac{c}{b}$
-
C.
$x \in R;y = \dfrac{c}{b}$
-
D.
$x \in R;y = - \dfrac{c}{b}$
Câu 2 :
Công thức nghiệm tổng quát của phương trình $3x + 0y = 12$
-
A.
$\left\{ \begin{array}{l}x \in \mathbb{R}\\y = - 4\end{array} \right.$
-
B.
$\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 4\end{array} \right.$
-
C.
$\left\{ \begin{array}{l}y \in \mathbb{R}\\x = - 4\end{array} \right.$
-
D.
$\left\{ \begin{array}{l}y \in \mathbb{R}\\x = 4\end{array} \right.$
Câu 3 :
Cho đường thẳng $d$ có phương trình $(m - 2)x + (3m - 1)y = 6m + 2$
Tìm các giá trị của tham số $m$ để $d$ song song với trục tung.
-
A.
$m = \dfrac{1}{3}$
-
B.
$m = \dfrac{2}{3}$
-
C.
$m \ne 2$
-
D.
$m \ne \dfrac{1}{3}$
Câu 4 :
Cho đường thẳng $d$ có phương trình $(m - 2)x + (3m - 1)y = 6m - 2$
Tìm các giá trị của tham số $m$ để $d$ đi qua gốc tọa độ.
-
A.
$m = \dfrac{1}{3}$
-
B.
$m = \dfrac{2}{3}$
-
C.
$m \ne 2$
-
D.
$m \ne \dfrac{1}{3}$
Câu 5 :
Chọn khẳng định đúng. Đường thẳng $d$ biểu diễn tập nghiệm của phương trình $3x - y = 3$ là
-
A.
Đường thẳng song song với trục hoành
-
B.
Đường thẳng song song với trục tung
-
C.
Đường thẳng đi qua gốc tọa độ
-
D.
Đường thẳng đi qua điểm $A\left( {1;0} \right)$
Câu 6 :
Cho đường thẳng nào dưới đây có biểu diễn hình học là đường thẳng song song với trục hoành?
-
A.
$5y = 7$
-
B.
$3x = 9$
-
C.
$x + y = 9$
-
D.
$6y + x = 7$
Câu 7 :
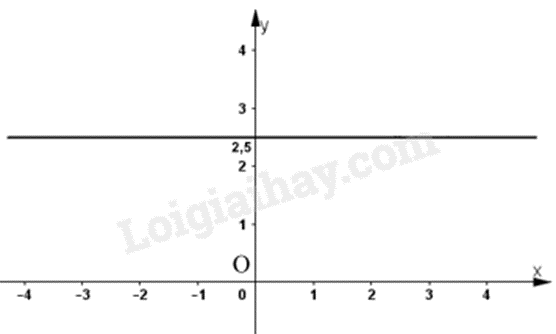
Chọn khẳng định đúng. Hình vẽ dưới đây biểu diễn tập nghiệm của phương trình nào?
-
A.
\(3x - y = 2\)
-
B.
\(x + 2y = 4\)
-
C.
\(x + 5y = 3\)
-
D.
\(0x + 2y = 5\)
Câu 8 :
Cho đường thẳng nào dưới đây có biểu diễn hình học là đường thẳng song song với trục tung?
-
A.
$y = - 2$
-
B.
$7x + 14 = 0$
-
C.
$x + 2y = 3$
-
D.
$y - x = 9$
-
A.
\(2x + y = 2\).
-
B.
\(2x - y = 2\).
-
C.
\(2x + y = - 2\).
-
D.
\(2x - y = - 2\).
Câu 10 :
Tập nghiệm của phương trình \(2x + 0y = 5\) được biểu diễn bởi
-
A.
đường thẳng \(y = 2x - 5\).
-
B.
đường thẳng \(y = \frac{5}{2}\).
-
C.
đường thẳng \(y = 5 - 2x\).
-
D.
đường thẳng \(x = \frac{5}{2}\).
Câu 11 :
Tập nghiệm của \(3x - 4y = - 1\) được biểu diễn bằng đường thẳng
-
A.
\(y = - 3x - 1\).
-
B.
\(y = \frac{3}{4}x + \frac{1}{4}\).
-
C.
\(y = 4x + 1\).
-
D.
\(y = \frac{3}{4}x - \frac{1}{4}\).
-
A.
\(2x + 0y = 5\).
-
B.
\(0x + 2y = 5\).
-
C.
\(0x - y = 2,5\).
-
D.
\( - 2x + 0y = 5\).
Câu 13 :
Phương trình \(x - 3y = 0\) có nghiệm tổng quát là:
-
A.
\(x \in \mathbb{R},y = 3x\).
-
B.
\(x = 3y,y \in \mathbb{R}\).
-
C.
\(x \in \mathbb{R},y = 3\).
-
D.
\(y \in \mathbb{R},x = 0\).
