Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn
Bài 2. Giải hệ hai phương trình bậc nhất hai ẩn
Luyện tập chung trang 19
Bài 3. Giải bài toán bằng cách lập hệ phương trình
Bài tập cuối chương 1
CHƯƠNG 2. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 4. Phương trình quy về phương trình bậc nhất một ẩn
Bài 5. Bất đẳng thức và tính chất
Luyện tập chung trang 36
Bài 6. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN BẬC HAI VÀ CĂN BẬC BA
Bài 7. Căn bậc hai và căn thức bậc hai
Bài 8. Khai căn bậc hai với phép nhân và phép chia
Luyện tập chung trang 52
Bài 9. Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai
Bài 10. Căn bậc ba và căn thức bậc ba
Luyện tập chung trang 63
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 11. Tỉ số lượng giác của góc nhọn
Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Luyện tập chung trang 79
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 13. Mở đầu về đường tròn
Bài 14. Cung và dây của một đường tròn
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
Luyện tập chung trang 96
Bài 16. Vị trí tương đối của đường thẳng và đường tròn
Bài 17. Vị trí tương đối của hai đường tròn
Luyện tập chung trang 108
Bài tập cuối chương 5
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 18. Hàm số y = ax^2 (a khác 0)
Bài 19. Phương trình bậc hai một ẩn
Luyện tập chung trang 18
Bài 20. Định lí Viète và ứng dụng
Bài 21. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 28
Bài tập cuối chương 6
CHƯƠNG 7. TẦN SỐ VÀ TẦN SỐ TƯƠNG ĐỐI
Bài 22. Bảng tần số và biểu đồ tần số
Bài 23. Bảng tần số tương đối và biểu đồ tần số tương đối
Luyện tập chung trang 43
Bài 24. Bảng tần số, tần số tương đối ghép nhóm và biểu đồ
Bài tập cuối chương 7
CHƯƠNG 8. XÁC SUẤT CỦA BIẾN CỐ TRONG MỘT SỐ MÔ HÌNH XÁC SUẤT ĐƠN GIẢN
Bài 25. Phép thử ngẫu nhiên và không gian mẫu
Bài 26. Xác suất của biến cố liên quan tới phép thử
Luyện tập chung trang 64
Bài tập cuối chương 8
CHƯƠNG 9. ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP
Bài 27. Góc nội tiếp
Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác
Luyện tập chung trang 78
Bài 29. Tứ giác nội tiếp
Bài 30. Đa giác đều
Luyện tập chung trang 90
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 31. Hình trụ và hình nón
Bài 32. Hình cầu
Luyện tập chung trang 106
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Pha chế dung dịch theo nồng độ yêu cầu
Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm Geogebra
Xác định tần số, tần số tương đối, vẽ các biểu đồ biểu diễn bảng tần số, tần số tương đối bằng Excel
Gene trội trong các thế hệ lai
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Diện tích hình quạt tròn Toán 9 có đáp án
Trắc nghiệm Diện tích hình quạt tròn
13 câu hỏi
Trắc nghiệm
Câu 1 :
Cho đường tròn $\left( {O,10\,cm} \right)$, đường kính $AB.$. Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {45^0}\). Tính diện tích hình quạt $AOM$ .
-
A.
\(5\pi (c{m^2})\)
-
B.
\(25\pi (c{m^2})\)
-
C.
\(50\pi (c{m^2})\)
-
D.
\(\dfrac{{25}}{2}\pi (c{m^2})\)
Câu 2 :
Cho đường tròn $\left( O \right)$ đường kính $AB = $ \(4\sqrt 3 \) $cm$ .
Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình viên phân$AC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
-
A.
\(\pi - 3\sqrt 3 \) $ cm^2$
-
B.
\(2\pi - 3\sqrt 3 \) $ cm^2$
-
C.
\(4\pi - 3\sqrt 3 \) $ cm^2$
-
D.
\(2\pi - \sqrt 3 \) $ cm^2$
Câu 3 :
Cho đường tròn $\left( O \right)$ đường kính \(AB = 2\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ .
-
A.
\(\pi - \sqrt 3 \)
-
B.
\(2\pi - 2\sqrt 3 \)
-
C.
\(\pi - 3\sqrt 3 \)
-
D.
\(2\pi - \sqrt 3 \)
Câu 5 :
Cho hình vuông \(ABCD\) có cạnh \(2R.\)
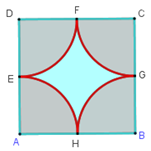
Diện tích \(S\) phần màu xanh trong hình vuông \(ABCD\) là
-
A.
\(S = 4{R^2} - \pi {R^2}\)
-
B.
\(S = \pi {R^2} - {R^2}\)
-
C.
\(S = 4{R^2} + \pi {R^2}\)
-
D.
\(S = 4\pi {R^2}\)
Câu 6 :
Cho đường tròn $\left( {O,8\,cm} \right)$, đường kính $AB.$ Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {60^0}\). Tính diện tích hình quạt $AOM$ .
-
A.
\(32\pi (c{m^2})\)
-
B.
\(\dfrac{{16\pi }}{3}(c{m^2})\)
-
C.
\(\dfrac{{32\pi }}{3}(c{m^2})\)
-
D.
\(23\pi (c{m^2})\)
Câu 7 :
Cho đường tròn $\left( O \right)$ đường kính $AB = $ $3\sqrt 3 $$cm$ . Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {60^0}\). Tính diện tích hình viên phân$BC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy)
-
A.
$\dfrac{{18\pi - 27\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$
-
B.
$\dfrac{{18\pi - 9\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$
-
C.
$\dfrac{{2\pi - 3\sqrt 3 }}{{16}}\left( {c{m^2}} \right)$
-
D.
$\dfrac{{18\pi - 27\sqrt 3 }}{4}\left( {c{m^2}} \right)$
Câu 8 :
Cho đường tròn $\left( O \right)$ đường kính \(AB = 4\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hai hình viên phân giới hạn bởi nửa đường tròn $\left( O \right)$ và dây $AC,BC$ .
-
A.
\(\pi - \sqrt 3 \)
-
B.
\(2\pi - 2\sqrt 3 \)
-
C.
\(\pi - 3\sqrt 3 \)
-
D.
\(2\pi - \sqrt 3 \)
Câu 10 :
Tại một vòng xoay ngã tư, người ta cần làm các bồn trồng hoa như hình 1. Em hãy tính phần diện tích của 1 bồn hoa ở hình 2 (phần được tô đậm). Biết rằng bán kính của vòng tròn lớn là 7m, vòng tròn nhỏ là 3m, số đo cung tròn đó là \(60^\circ \). (làm tròn đến hàng phần mười)
-
A.
\(20,9{m^2}\).
-
B.
\(41,9{m^2}\).
-
C.
\(2,1{m^2}\).
-
D.
\(10,5{m^2}\).
Câu 11 :
Máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước. Khi bơm căng, bánh xe sau có đường kính là 1,672m và bánh xe trước có đường kính là 88cm. Hỏi khi bánh xe sau lăn được 10 vòng thì bánh xe trước lăn được mấy vòng?
-
A.
\(\frac{{19}}{2}\).
-
B.
\(19\).
-
C.
\(38\).
-
D.
\(20\).
Câu 12 :
Khi căng một chiếc quạt giấy ta được một hình quạt với kích thước như hình vẽ minh họa. Hãy tính diện tích phần giấy để làm một cái quạt (không tính mép và phần thừa). Làm tròn kết quả tới chữ số thập phân thứ 2.
-
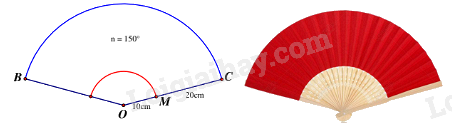
A.
\(130,69c{m^2}\).
-
B.
\(392,69c{m^2}\).
-
C.
\(1047,20c{m^2}\).
-
D.
\(654,50c{m^2}\).
Câu 13 :
Một hình quạt tròn có bán kính 6cm, số đo cung là \(36^\circ \). Diện tích hình quạt tròn đó là
-
A.
\(3,6\pi \left( {cm} \right)\).
-
B.
\(3,6\pi \left( {c{m^2}} \right)\).
-
C.
\(7,2\pi \left( {c{m^2}} \right)\).
-
D.
\(6\pi \left( {c{m^2}} \right)\).
CÁC BÀI TẬP KHÁC
