Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn
Bài 2. Giải hệ hai phương trình bậc nhất hai ẩn
Luyện tập chung trang 19
Bài 3. Giải bài toán bằng cách lập hệ phương trình
Bài tập cuối chương 1
CHƯƠNG 2. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 4. Phương trình quy về phương trình bậc nhất một ẩn
Bài 5. Bất đẳng thức và tính chất
Luyện tập chung trang 36
Bài 6. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN BẬC HAI VÀ CĂN BẬC BA
Bài 7. Căn bậc hai và căn thức bậc hai
Bài 8. Khai căn bậc hai với phép nhân và phép chia
Luyện tập chung trang 52
Bài 9. Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai
Bài 10. Căn bậc ba và căn thức bậc ba
Luyện tập chung trang 63
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 11. Tỉ số lượng giác của góc nhọn
Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Luyện tập chung trang 79
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 13. Mở đầu về đường tròn
Bài 14. Cung và dây của một đường tròn
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
Luyện tập chung trang 96
Bài 16. Vị trí tương đối của đường thẳng và đường tròn
Bài 17. Vị trí tương đối của hai đường tròn
Luyện tập chung trang 108
Bài tập cuối chương 5
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 18. Hàm số y = ax^2 (a khác 0)
Bài 19. Phương trình bậc hai một ẩn
Luyện tập chung trang 18
Bài 20. Định lí Viète và ứng dụng
Bài 21. Giải bài toán bằng cách lập phương trình
Luyện tập chung trang 28
Bài tập cuối chương 6
CHƯƠNG 7. TẦN SỐ VÀ TẦN SỐ TƯƠNG ĐỐI
Bài 22. Bảng tần số và biểu đồ tần số
Bài 23. Bảng tần số tương đối và biểu đồ tần số tương đối
Luyện tập chung trang 43
Bài 24. Bảng tần số, tần số tương đối ghép nhóm và biểu đồ
Bài tập cuối chương 7
CHƯƠNG 8. XÁC SUẤT CỦA BIẾN CỐ TRONG MỘT SỐ MÔ HÌNH XÁC SUẤT ĐƠN GIẢN
Bài 25. Phép thử ngẫu nhiên và không gian mẫu
Bài 26. Xác suất của biến cố liên quan tới phép thử
Luyện tập chung trang 64
Bài tập cuối chương 8
CHƯƠNG 9. ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP
Bài 27. Góc nội tiếp
Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác
Luyện tập chung trang 78
Bài 29. Tứ giác nội tiếp
Bài 30. Đa giác đều
Luyện tập chung trang 90
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 31. Hình trụ và hình nón
Bài 32. Hình cầu
Luyện tập chung trang 106
Bài tập cuối chương 10
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Pha chế dung dịch theo nồng độ yêu cầu
Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra
Vẽ hình đơn giản với phần mềm Geogebra
Xác định tần số, tần số tương đối, vẽ các biểu đồ biểu diễn bảng tần số, tần số tương đối bằng Excel
Gene trội trong các thế hệ lai
BÀI TẬP ÔN TẬP CUỐI NĂM
Bài tập ôn tập cuối năm
Trắc nghiệm Bài tập Bài 16. Vị trí tương đối của đường thẳng và đường tròn Toán 9 có đáp án
Trắc nghiệm Bài tập Bài 16. Vị trí tương đối của đường thẳng và đường tròn
34 câu hỏi
Trắc nghiệm
Câu 1 :
Cho $\left( {O;5cm} \right)$. Đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;5\,cm} \right)$, khi đó
-
A.
Khoảng cách từ $O$ đến đường thẳng $d$ nhỏ hơn $5\,cm$
-
B.
Khoảng cách từ $O$ đến đường thẳng $d$ lớn hơn $5\,cm$
-
C.
Khoảng cách từ $O$ đến đường thẳng $d$ bằng $5\,cm$
-
D.
Khoảng cách từ $O$ đến đường thẳng $d$ bằng $6\,cm$
Câu 2 :
Cho tam giác $ABC$ có $AC = 3cm,AB = 4cm,BC = 5cm$. Vẽ đường tròn $\left( {C;CA} \right)$. Khẳng định nào sau đây là đúng?
-
A.
Đường thẳng $BC$ cắt đường tròn $\left( {C;CA} \right)$ tại một điểm
-
B.
$AB$ là cát tuyến của đường tròn $\left( {C;CA} \right)$
-
C.
$AB$ là tiếp tuyến của $\left( {C;CA} \right)$
-
D.
$BC$ là tiếp tuyến của $\left( {C;CA} \right)$
Câu 3 :
Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.
-
A.
$HK$
-
B.
$IB$
-
C.
$IC$
-
D.
$AC$
Câu 4 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Đường tròn đường kính $BH$ cắt $AB$ tại $D$, đường tròn đường kính $CH$ cắt $AC$ tại $E$ . Chọn khẳng định sai trong các khẳng định sau
-
A.
$DE$ là cắt đường tròn đường kính $BH$
-
B.
$DE$ là tiếp tuyến của đường tròn đường kính $BH$
-
C.
Tứ giác$AEHD$ là hình chữ nhật
-
D.
$DE \bot DI$ (với $I$ là trung điểm $BH$)
Câu 9 :
Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :
|
$R$ |
$d$ |
Vị trí tương đối của đường thẳng và đường tròn |
|
$5cm$ |
$\,4\,cm$ |
...............$\left( 1 \right)$................... |
|
$8cm$ |
...$\left( 2 \right)$... |
Tiếp xúc nhau |
-
A.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
B.
$\left( 1 \right)$ : $9\,cm$; $\left( 2 \right)$ : cắt nhau
-
C.
$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $8\,cm$
-
D.
$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $6\,cm$
Câu 10 :
Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.
-
A.
Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
-
B.
Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
-
C.
Cả hai trục tọa độ đều cắt đường tròn
-
D.
Cả hai trục tọa độ đều tiếp xúc với đường tròn.
Câu 11 :
Cho $a,b$ là hai đường thẳng song song và cách nhau một khoảng $2,5\,cm$. Lấy điểm $I$ trên $a$ và vẽ đường tròn $\left( {I;2,5cm} \right)$. Khi đó đường tròn với đường thẳng $b$
-
A.
cắt nhau
-
B.
không cắt nhau
-
C.
tiếp xúc
-
D.
đáp án khác
Câu 12 :
Cho góc $\widehat {xOy}\,\left( {0 < \widehat {xOy} < 180^\circ } \right)$. Đường tròn $\left( I \right)$ là đường tròn tiếp xúc với cả hai cạnh $Ox;Oy$. Khi đó điểm $I$ chạy trên đường nào?
-
A.
Đường thẳng vuông góc với $Ox$ tại $O$
-
B.
Tia phân giác của góc $\widehat {xOy}$
-
C.
Tia $Oz$ nằm giữa $Ox$ và $Oy$
-
D.
Tia phân giác của góc $\widehat {xOy}$ trừ điểm $O$
Câu 13 :
Cho đường tròn tâm $O$ bán kính $3cm$ và một điểm $A$ cách $O$ là $5cm$. Kẻ tiếp tuyến $AB$ với đường tròn ( $B$ là tiếp điểm). Tính độ dài $AB$.
-
A.
$AB = \,3\,cm$
-
B.
$AB = \,4\,cm$
-
C.
$AB = \,5\,cm$
-
D.
$AB = \,2\,cm$
Câu 14 :
Cho đường tròn $\left( {O;R} \right)$ và dây $AB = 1,2R$. Vẽ một tiếp tuyến song song với $AB$, cắt các tia $OA,OB$ lần lượt tại $E$ và $F$. Tính diện tích tam giác $OEF$ theo $R$.
-
A.
${S_{OEF}} = 0,75{R^2}$
-
B.
${S_{OEF}} = 1,5{R^2}$
-
C.
${S_{OEF}} = 0,8{R^2}$
-
D.
${S_{OEF}} = 1,75{R^2}$
Câu 15 :
Cho hai đường thẳng $a$ và $b$ song song với nhau, cách nhau một khoảng là $h$. Một đường tròn $\left( O \right)$ tiếp xúc với $a$ và $b$. Hỏi tâm $O$ di động trên đường nào?
-
A.
Đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{h}{2}$.
-
B.
Đường thẳng $c$ song song và cách đều $a,b$ một khoảng $\dfrac{{2h}}{3}$.
-
C.
Đường thẳng $c$ đi qua $O$ vuông góc với $a,b$
-
D.
Đường tròn $\left( {A;AB} \right)$ với $A,B$ lần lượt là tiếp điểm của $a,b$ với $\left( O \right)$.
Câu 17 :
Hai tiếp tuyến tại $A$ và $B$ của đường tròn $(O)$ cắt nhau tại $I$ . Đường thẳng qua $I$ và vuông góc với $IA$ cắt $OB$ tại $K$. Chọn khẳng định đúng.
-
A.
$OI = OK = KI$
-
B.
$KI = KO$
-
C.
$OI = OK$
-
D.
$IO = IK$
Câu 18 :
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
-
A.
$18\,cm$
-
B.
$6\sqrt 3 cm$
-
C.
$12\sqrt 3 \,cm$
-
D.
$15\,cm$
Câu 20 :
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
-
A.
$AC = CB$
-
B.
$\widehat {CBO'} = 90^\circ $
-
C.
$CA,CB$ là hai tiếp tuyến của $\left( {O'} \right)$
-
D.
$CA,CB$ là hai cát tuyến của $\left( {O'} \right)$
Câu 23 :
Cho đường tròn $\left( {O;3cm} \right)$, lấy điểm $A$ sao cho $OA = 6cm$. Từ \(A\) vẽ tiếp tuyến $AB,AC$ đến đường tròn $\left( O \right)$ ($B,C$ là tiếp điểm). Chu vi tam giác $ABC$ là
-
A.
$9cm$
-
B.
$9\sqrt 3 cm$
-
C.
$9\sqrt 2 cm$
-
D.
Kết quả khác
Câu 24 :
Hai tiếp tuyến tại $A$ và $B$ của đường tròn $\left( {O;R} \right)$ cắt nhau tại $M.$ Nếu $MA = \;R\sqrt 3 $ thì góc $\widehat {AOB}$ bằng:
-
A.
${120^0}\;$
-
B.
${90^0}$
-
C.
${60^0}$
-
D.
${45^0}$
Câu 25 :
Cho tam giác $ABC$ có $AB = 5,AC = 12,BC = 13$. Khi đó:
-
A.
$AB$ là tiếp tuyến của đường tròn $\left( {C;5} \right)$
-
B.
$AC$ là tiếp tuyến của đường tròn $\left( {B;5} \right)$
-
C.
$AB$ là tiếp tuyến của đường tròn $\left( {B;12} \right)$
-
D.
$AC$ là tiếp tuyến của đường tròn $\left( {C;13} \right)$
Câu 26 :
Hai tiếp tuyến tại hai điểm $B,C$ của một đường tròn $\left( O \right)$ cắt nhau tại $A$ tạo thành \(\widehat {BAC} = {50^0}\). Số đo của góc \(\widehat {BOC}\) bằng
-
A.
${30^0}$
-
B.
${40^0}$
-
C.
${130^0}$
-
D.
${310^0}$
Câu 27 :
Cho hình vẽ, biết số đo cung \(BmD\) là \({120^0}.\) Khi đó
-
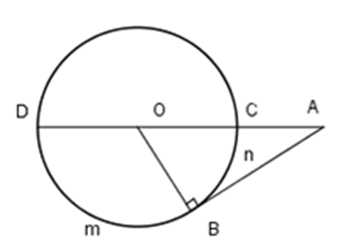
A.
\(\widehat {OAB} = {75^0}\)
-
B.
\(\widehat {OAB} = {60^0}\)
-
C.
\(\widehat {OAB} = {45^0}\)
-
D.
\(\widehat {OAB} = {30^0}\)
Câu 28 :
Cho nửa đường tròn (O ; R), AB là đường kính. Dây BC có độ dài R. Trên tia đối của tia CB lấy điểm D sao cho \(CD = 3R. \) Chọn câu đúng.
-
A.
AD là tiếp tuyến của đường tròn.
-
B.
\(\widehat {ACB} = 90^\circ \)
-
C.
\(AD\) cắt đường tròn \(\left( {O;R} \right)\) tại hai điểm phân biệt
-
D.
Cả A, B đều đúng.
Câu 29 :
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên AO lấy điểm M sao cho \(AM = AB.\) Các tia BM và CM lần lượt cắt đường tròn tại một điểm thứ hai là D và E. Chọn câu đúng.
-
A.
M là tâm đường tròn ngoại tiếp tam giác OBC
-
B.
DE là đường kính của đường tròn (O)
-
C.
M là tâm đường tròn nội tiếp tam giác OBC
-
D.
Cả A, B, C đều sai
Câu 30 :
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
-
A.
\(2,4cm\)
-
B.
\(4,8cm\)
-
C.
\(\dfrac{5}{{12}}cm\)
-
D.
\(5cm\)
Câu 31 :
Đường thẳng \(a\) cách tâm \(O\) của đường tròn \(\left( {O;R} \right)\)một khoảng bằng \(\sqrt 8 \,\,cm.\) Biết \(R = 3\,\,cm,\) số giao điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) là:
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\).
Câu 32 :
Hai tiếp tuyến tại hai điểm \(B,C\) của một đường tròn \(\left( O \right)\) cắt nhau tại \(A\) tạo thành \(\widehat {BAC} = {50^0}\). Số đo của góc \(\widehat {BOC}\) chắn cung nhỏ \(BC\) bằng
-
A.
\({30^0}\)
-
B.
\({40^0}\)
-
C.
\({130^0}\)
-
D.
\({310^0}\)
Câu 33 :
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài tại \(A\). Kẻ tiếp tuyến chung ngoài \(BC,B \in \left( O \right)\) và \(C \in (O')\). Tiếp tuyến chung trong tại \(A\) cắt tiếp tuyến chung ngoài \(BC\) tại \(I\). Tính độ dài \(BC\) biết \(OA = 9cm,O'A = 4cm\).
-
A.
\(12cm\)
-
B.
\(18cm\)
-
C.
\(10cm\)
-
D.
\(6cm\)
Câu 34 :
Khoảng cách từ điểm O đến đường thẳng a bằng 7cm. Khẳng định nào sau đây là sai?
-
A.
Đường thẳng a tiếp xúc với đường tròn (O; 7cm).
-
B.
Đường thẳng a cắt đường tròn (O; 5cm).
-
C.
Đường thẳng a không giao với đường tròn (O; 5cm).
-
D.
Đường thẳng a cắt đường tròn tâm (O; 8cm).
CÁC BÀI TẬP KHÁC
