Trắc nghiệm Cung, số đo cung Toán 9 có đáp án
Trắc nghiệm Cung, số đo cung
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
-
A.
$AD > BC$
-
B.
Số đo cung $AD$ bằng số đo cung $BC$
-
C.
$AD < BC$
-
D.
$\widehat {AOD} > \widehat {COB}$
Chọn khẳng định đúng. Trong một đường tròn, số đo cung nhỏ bằng
-
A.
Số đo cung lớn
-
B.
Số đo của góc ở tâm chắn cung đó
-
C.
Số đo của góc ở tâm chắn cung lớn
-
D.
Số đo của cung nửa đường tròn
Trong hai cung của một đường tròn hay hai đường tròn bằng nhau, cung nào nhỏ hơn
-
A.
Có số đo lớn hơn
-
B.
Có số đo nhỏ hơn $90^\circ $
-
C.
Có số đo lớn hơn $90^\circ $
-
D.
Có số đo nhỏ hơn
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là trung điểm của bán kính \(OA\). Dây \(CD\) vuông góc với \(OA\) tại $H$ . Tính số đo cung lớn \(CD.\)
-
A.
$260^\circ $
-
B.
$300^\circ $
-
C.
$240^\circ $
-
D.
$120^\circ $
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 55^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
-
A.
$55^\circ $
-
B.
$60^\circ $
-
C.
$40^\circ $
-
D.
$50^\circ $
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
-
A.
Cung $AB$ lớn hơn cung $CD$
-
B.
Cung $AB$ nhỏ hơn cung $CD$
-
C.
Cung $AB$ bằng cung $CD$
-
D.
Số đo cung $AB$ bằng hai lần số đo cung $CD$
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
-
A.
$AD > BC$
-
B.
Số đo cung $AD$ bằng số đo cung $BC$
-
C.
$AD < BC$
-
D.
$\widehat {AOD} > \widehat {COB}$
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
-
A.
$AC = BE$
-
B.
Số đo cung$AD$ bằng số đo cung $BE$
-
C.
Số đo cung $AC$ bằng số đo cung $BE$
-
D.
$\widehat {AOC} < \widehat {AOD}$
Chọn khẳng định đúng.
-
A.
Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
B.
Trong một đường tròn, đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
C.
Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì song song với dây căng cung ấy
-
D.
Trong một đường tròn, hai đường kính luôn vuông góc với nhau
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
-
A.
$AB$
-
B.
$AC$
-
C.
$BC$
-
D.
$AB,AC$
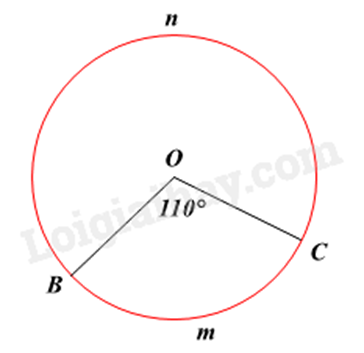
Số đo cung lớn \(BnC\) trong hình bên là:

-
A.
\({280^0}\)
-
B.
\({290^0}\)
-
C.
\({300^0}\)
-
D.
\({310^0}\)
Chọn khẳng định đúng. Trong một đường tròn, số đo cung lớn bằng
-
A.
Số đo cung nhỏ
-
B.
Hiệu giữa \({360^0}\) và số đo của cung nhỏ (có chung $2$ mút với cung lớn).
-
C.
Tổng giữa \({360^0}\) và số đo của cung nhỏ (có chung $2$ mút với cung lớn).
-
D.
Số đo của cung nửa đường tròn
Chọn câu đúng. Trong hai cung của một đường tròn hay hai đường tròn bằng nhau,
-
A.
Hai cung bằng nhau nếu chúng đều là cung nhỏ
-
B.
Hai cung bằng nhau nếu chúng số đo nhỏ hơn $90^\circ $
-
C.
Hai cung bằng nhau nếu chúng đều là cung lớn
-
D.
Hai cung bằng nhau nếu chúng có số đo bằng nhau
Cho đường tròn \(\left( {O;R} \right).\) Gọi \(H\) là điểm thuộc bán kính \(OA\) sao cho \(OH = \dfrac{{\sqrt 3 }}{2}OA\) . Dây \(CD\) vuông góc với \(OA\) tại $H.$ Tính số đo cung lớn \(CD.\)
-
A.
$260^\circ $
-
B.
$300^\circ $
-
C.
$240^\circ $
-
D.
$120^\circ $
Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) vẽ góc ở tâm \(\widehat {AOC} = 60^\circ \) . Vẽ dây \(CD\) vuông góc với \(AB\) và dây \(DE\) song song với \(AB.\) Tính số đo cung nhỏ \(BE\)
-
A.
$120^\circ $
-
B.
$60^\circ $
-
C.
$240^\circ $
-
D.
$30^\circ $
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có cung $MN < $ cung \(PQ\), khi đó
-
A.
\(MN > PQ\)
-
B.
\(MN < PQ\)
-
C.
\(MN = PQ\)
-
D.
\(PQ = 2MN\)
Cho đường tròn (O) đường kính $AB$ và một cung $AC$ có số đo bằng $50^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
-
A.
$AD = DE = BE$
-
B.
Số đo cung$AE$ bằng số đo cung $BD$
-
C.
Số đo cung$AC$ bằng số đo cung $BE$
-
D.
$\widehat {AOC} = \widehat {AOD} = \widehat {BOE} = 50^\circ $
Chọn khẳng định sai.
-
A.
Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
-
B.
Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
-
C.
Trong một đường tròn, cung lớn hơn căng dây lớn hơn.
-
D.
Trong một đường tròn, hai đường kính luôn bằng nhau và vuông góc với nhau.
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 70^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung nhỏ nhất?
-
A.
Cung $AB$
-
B.
Cung $AC$
-
C.
Cung $BC$
-
D.
Cung $AB$, cung \(AC.\)
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 2 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
-
A.
$MN = R\sqrt 3 $
-
B.
$MN = R\sqrt 2 $
-
C.
$MN = \left( {2 + \sqrt 2 } \right)R$
-
D.
$MN = R\sqrt {2 + \sqrt 2 } $
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là sai?
-
A.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2} + B{C^2}$
-
B.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{D^2} + A{C^2}$
-
C.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{E^2}$
-
D.
$I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2}$
Cho đường tròn (O;R) có dây AB = R. Số đo góc ở tâm \(\widehat {AOB}\) và cung lớn AB là:
-
A.
\(\widehat {AOB} = 60^\circ \), số đo cung lớn AB là \(240^\circ \).
-
B.
\(\widehat {AOB} = 120^\circ \), số đo cung lớn AB là \(240^\circ \).
-
C.
\(\widehat {AOB} = 60^\circ \), số đo cung lớn AB là \(300^\circ \).
-
D.
\(\widehat {AOB} = 120^\circ \), số đo cung lớn AB là \(300^\circ \).
Chọn khẳng định sai.
-
A.
Số đo của nửa đường tròn bằng \(180^\circ \).
-
B.
Số đo của cung lớn bằng thương của \(360^\circ \) và số đo của cung nhỏ có chung hai mút.
-
C.
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
-
D.
Số đo của cung AB được kí hiệu là $\overset\frown{AB}$.
Cung cả đường tròn có số đo
-
A.
\(360^\circ \).
-
B.
\(270^\circ \).
-
C.
\(180^\circ \).
-
D.
\(90^\circ \).
-
A.
\(110^\circ \).
-
B.
\(220^\circ \).
-
C.
\(140^\circ \).
-
D.
\(250^\circ \).
Cho đường tròn (O) có AB là đường kính. Lấy C là điểm thuộc cung cung AB biết \(\widehat {AOC} = 130^\circ \). Số đo cung nhỏ \(BC\) là:

-
A.
\(360^\circ \).
-
B.
\(230^\circ \).
-
C.
\(130^\circ \).
-
D.
\(50^\circ \).
CÁC BÀI TẬP KHÁC