Trắc nghiệm Bài tập Bài 27. Góc nội tiếp Toán 9 có đáp án
Trắc nghiệm Bài tập Bài 27. Góc nội tiếp
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
-
A.
\(AD.AE\)
-
B.
\(AD.AC\)
-
C.
\(AE.BE\)
-
D.
\(AD.BD\)
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
-
A.
\(AH.HD\)
-
B.
$AH.AD$
-
C.
\(AH.HB\)
-
D.
$A{H^2}$
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
-
A.
\(13,5\,cm\)
-
B.
$12\,cm$
-
C.
\(18\,cm\)
-
D.
$6\,cm$
Cho hình vẽ (hai đường tròn có tâm là \(B,C \) và điểm \(B\) nằm trên đường tròn tâm \(C\)). Biết $\widehat {MAN} = {20^0}.$
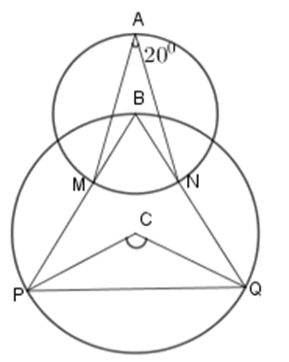
Khi đó \(\widehat {PCQ} = ?\)
-
A.
\({60^0}\)
-
B.
\({70^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Cho đường tròn \(\left( O \right)\) Trên \(\left( O \right)\) lấy ba điểm \(A,B,D\) sao cho \(\widehat {AOB} = {120^0},\,\,AD = BD.\)
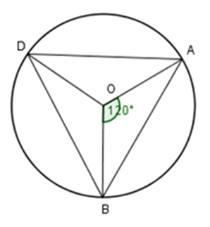
Khi đó \(\Delta ABD\) là:
-
A.
Tam giác đều.
-
B.
Tam giác vuông tại \(D\)
-
C.
Tam giác vuông cân tại \(D\)
-
D.
Tam giác vuông tại \(A\).
Cho bốn điểm A, B, C, D thuộc đường tròn \(\left( O \right).\) Biết \(\widehat {BOD} = {130^0}\) thì số đo \(\widehat {BAD}\) là:
-
A.
\({50^0}\)
-
B.
\({130^0}\)
-
C.
\({15^0}\)
-
D.
\({65^0}\)
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
-
A.
Hình bình hành
-
B.
Hình thang
-
C.
Hình thang cân
-
D.
Hình thoi
Cho hình vẽ. Khi đó đáp án đúng là
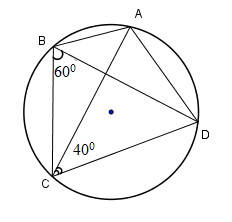
-
A.
\(\widehat {ADC} = {70^0}\)
-
B.
\(\widehat {ADC} = {80^0}\)
-
C.
\(\widehat {ADC} = {75^0}\)
-
D.
\(\widehat {ADC} = {60^0}\)
Tam giác $ABC$ nằm trên đường tròn $\left( {O;R} \right)$ biết góc $\widehat C = {45^o}$ và $AB = a$. Bán kính đường tròn $\left( O \right)$ là
-
A.
\(a\sqrt 2 \)
-
B.
\(a\sqrt 3 \)
-
C.
\(\dfrac{{a\sqrt 2 }}{2}\)
-
D.
$\dfrac{{a\sqrt 3 }}{3}$
Cho tam giác ABC nội tiếp đường tròn (O). Biết \(\widehat {BOC} = 120^\circ \) và \(\widehat {OCA} = 40^\circ \). Tính số đo góc BAO.
-
A.
\(40^\circ \).
-
B.
\(60^\circ \).
-
C.
\(20^\circ \).
-
D.
\(80^\circ \).






