CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

Bài 2. Giải hệ hai phương trình bậc nhất hai ẩn

Luyện tập chung trang 19

Bài 3. Giải bài toán bằng cách lập hệ phương trình

Bài tập cuối chương 1

CHƯƠNG 2. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN

Bài 4. Phương trình quy về phương trình bậc nhất một ẩn

Bài 5. Bất đẳng thức và tính chất

Luyện tập chung trang 36

Bài 6. Bất phương trình bậc nhất một ẩn

Bài tập cuối chương 2

CHƯƠNG 3. CĂN BẬC HAI VÀ CĂN BẬC BA

Bài 7. Căn bậc hai và căn thức bậc hai

Bài 8. Khai căn bậc hai với phép nhân và phép chia

Luyện tập chung trang 52

Bài 9. Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

Bài 10. Căn bậc ba và căn thức bậc ba

Luyện tập chung trang 63

Bài tập cuối chương 3

CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG

Bài 11. Tỉ số lượng giác của góc nhọn

Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Luyện tập chung trang 79

Bài tập cuối chương 4

CHƯƠNG 5. ĐƯỜNG TRÒN

Bài 13. Mở đầu về đường tròn

Bài 14. Cung và dây của một đường tròn

Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Luyện tập chung trang 96

Bài 16. Vị trí tương đối của đường thẳng và đường tròn

Bài 17. Vị trí tương đối của hai đường tròn

Luyện tập chung trang 108

Bài tập cuối chương 5

CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0). PHƯƠNG TRÌNH BẬC HAI MỘT ẨN

Bài 18. Hàm số y = ax^2 (a khác 0)

Bài 19. Phương trình bậc hai một ẩn

Luyện tập chung trang 18

Bài 20. Định lí Viète và ứng dụng

Bài 21. Giải bài toán bằng cách lập phương trình

Luyện tập chung trang 28

Bài tập cuối chương 6

CHƯƠNG 7. TẦN SỐ VÀ TẦN SỐ TƯƠNG ĐỐI

Bài 22. Bảng tần số và biểu đồ tần số

Bài 23. Bảng tần số tương đối và biểu đồ tần số tương đối

Luyện tập chung trang 43

Bài 24. Bảng tần số, tần số tương đối ghép nhóm và biểu đồ

Bài tập cuối chương 7

CHƯƠNG 8. XÁC SUẤT CỦA BIẾN CỐ TRONG MỘT SỐ MÔ HÌNH XÁC SUẤT ĐƠN GIẢN

Bài 25. Phép thử ngẫu nhiên và không gian mẫu

Bài 26. Xác suất của biến cố liên quan tới phép thử

Luyện tập chung trang 64

Bài tập cuối chương 8

CHƯƠNG 9. ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP

Bài 27. Góc nội tiếp

Bài 28. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

Luyện tập chung trang 78

Bài 29. Tứ giác nội tiếp

Bài 30. Đa giác đều

Luyện tập chung trang 90

Bài tập cuối chương 9

CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN

Bài 31. Hình trụ và hình nón

Bài 32. Hình cầu

Trắc nghiệm Bài tập Hình cầu

Luyện tập chung trang 106

Bài tập cuối chương 10

HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM

Pha chế dung dịch theo nồng độ yêu cầu

Giải phương trình, hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra

Vẽ hình đơn giản với phần mềm Geogebra

Xác định tần số, tần số tương đối, vẽ các biểu đồ biểu diễn bảng tần số, tần số tương đối bằng Excel

Gene trội trong các thế hệ lai

BÀI TẬP ÔN TẬP CUỐI NĂM

Bài tập ôn tập cuối năm

Trắc nghiệm Bài tập Hình cầu Toán 9 có đáp án

Trắc nghiệm Bài tập Hình cầu

17 câu hỏi

Trắc nghiệm

Câu 1 :

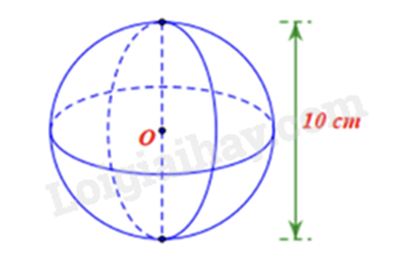
Một hình cầu có đường kính là 10cm. Bán kính của hình cầu là:

A.

$10\,{\rm{cm}}$.
B.

$5\,{\rm{cm}}$.
C.

$\sqrt 5 \,{\rm{cm}}$.
D.

$20\,{\rm{cm}}$.

Câu 2 :

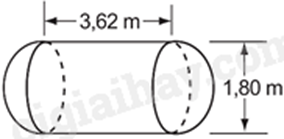
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ. Bán kính của hai nửa hình cầu là

A.

0,9m.
B.

1,8m.
C.

0,6m.
D.

1,2m.

Câu 3 :

Trái Đất của chúng ta được xem là có dạng hình cầu, có bán kính là R. Khi đó bán kính của đường xích đạo là

A.

$2R$.
B.

$\frac{R}{2}$.
C.

$4R$.
D.

R.

Câu 4 :

Cho hình cầu có đường kính $d = 6cm$. Diện tích mặt cầu là

A.

$36\pi \,(c{m^2})$
B.

$9\pi (c{m^2})$
C.

$12\pi (c{m^2})$
D.

$36\pi (cm)$

Câu 6 :

Cho hình cầu có thể tích $V = 288\pi (c{m^3})$. Tính đường kính mặt cầu của hình cầu đó.

A.

6cm.
B.

12cm.
C.

8cm.
D.

16cm.

Câu 7 :

Một bình chia độ hình trụ chứa 200 cm³ nước. Người ta bỏ lọt vào bình và chìm trong nước một khối kim loại hình cầu. Khi nước yên lặng, người ta thấy nước dâng lên vạch 313,04 cm³. Bán kính của khối kim loại hình cầu là: (Lấy $\pi \approx 3,14$).

A.

1cm.
B.

2cm.
C.

3cm.
D.

4cm.

Câu 10 :

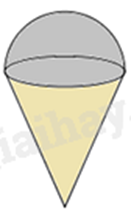
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Biết bán kính hình cầu và bán kính hình nón bằng nhau và bằng 2,5 cm; chiều cao của hình nón gấp 3 lần bán kính hình cầu. Tính thể tích của que kem? (Lấy $\pi = 3,14$ và làm tròn kết quả đến hàng đơn vị).

A.

$55\left( {c{m^3}} \right)$
B.

$82\left( {c{m^3}} \right)$
C.

$28\left( {c{m^3}} \right)$
D.

$85\left( {c{m^3}} \right)$

Câu 11 :

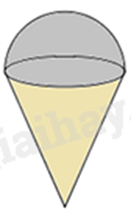
Một cơ sở sản xuất kem chuẩn bị làm 500 chiếc kem theo đơn đặt hàng. Cốc đựng kem có bề dày không đáng kể dạng hình nón chiều cao 10 cm, đường kính miệng cốc bằng 6 cm. Kem được đổ đầy vào cốc và dư ra phía ngoài một lượng có dạng nửa hình cầu có bán kính bằng bán kính miệng cốc (xem hình). Tính lượng kem cần dùng?