Bài 9. Hình chữ nhật

Phần câu hỏi bài 9 trang 121 Vở bài tập toán 8 tập 1

Giải phần câu hỏi bài 9 trang 121 VBT toán 8 tập 1. Đúng ghi Đ, sai ghi S vào ô trống. (A) Trong hình chữ nhật, hai đường chéo bằng nhau...

Lựa chọn câu để xem lời giải nhanh hơn

Câu 23.

Đúng ghi Đ, sai ghi S vào ô trống.

(A) Trong hình chữ nhật, hai đường chéo bằng nhau.

(B) Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.

(D) Giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.

Phương pháp giải:

Sử dụng:

- Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

- Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

- Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.

Lời giải chi tiết:

A) Đ

B) S

VD: Hình thang cân có hai đường chéo bằng nhau.

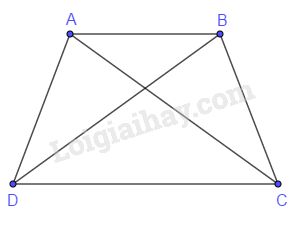
C) Đ

D) Đ

Hình chữ nhật cũng là một hình bình hành nên nhận giao điểm của hai đường chéo là tâm đối xứng.

Câu 24.

Đúng ghi Đ, sai ghi S vào ô trống.

(A) Hình thang \(ABCD\) có \(\widehat A = {90^o}\) là hình chữ nhật.

(B) Hình thang cân \(ABCD\) có \(\widehat A = {90^o}\) là hình chữ nhật.

Phương pháp giải:

Dấu hiệu nhận biết

a) Tứ giác có ba góc vuông là hình chữ nhật.

b) Hình thang cân có một góc vuông là hình chữ nhật.

c) Hình bình hành có một góc vuông là hình chữ nhật.

d) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Lời giải chi tiết:

(A) S

VD: Hình thang vuông chưa chắc đã là hình chữ nhật.

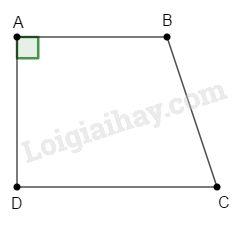
(B) Đ (theo dấu hiệu nhận biết hình chữ nhật)

Câu 25.

Tam giác \(ABC\) có \(AB=6, BC=8, AC =10.\) Độ dài đường trung tuyến kẻ từ \(B\) bằng

(A) \(4\) (B) \(10\)

Phương pháp giải:

- Định lí: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

- Định lí Pytago đảo: Trong một tam giác bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

Lời giải chi tiết:

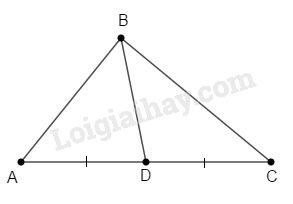
Gọi \(D\) là trung điểm của \(AC\)

Ta có \(A{B^2} + B{C^2} = {6^2} + {8^2} = 100\)\( = {10^2} = A{C^2}\)

Theo định lí Pytago đảo thì tam giác \(ABC\) vuông tại \(B\).

Áp dụng định lí: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền và tam giác \(ABC\) vuông tại \(B\) ta có:

\(BD=AC:2=10:2=5.\)

Chọn D.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 8 phiếu

Bài tiếp theo

Bài 39 trang 121 Vở bài tập toán 8 tập 1
Giải bài 39 trang 121 VBT toán 8 tập 1. Chứng minh rằng: a) Giao điểm hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó...
Bài 40 trang 122 Vở bài tập toán 8 tập 1
Giải bài 40 trang 122 VBT toán 8 tập 1. Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì ? Vì sao ?
Bài 41 trang 122 Vở bài tập toán 8 tập 1
Giải bài 41 trang 122 VBT toán 8 tập 1. Các câu sau đúng hay sai ? a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB...
Bài 42 trang 123 Vở bài tập toán 8 tập 1
Giải bài 42 trang 123 VBT toán 8 tập 1. Tìm x trên hình 57.
Bài 43 trang 123 Vở bài tập toán 8 tập 1
Giải bài 43 trang 123 VBT toán 8 tập 1. Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 59. Chứng minh rằng EFGH là hình chữ nhật.
Bài 44 trang 124 Vở bài tập toán 8 tập 1
Giải bài 44 trang 124 VBT toán 8 tập 1. Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?