Phần câu hỏi bài 4 trang 102 Vở bài tập toán 8 tập 1
Giải phần câu hỏi bài 4 trang 101 VBT toán 8 tập 1. Cho tam giác ABC. Đường thẳng a cắt BC ở D...
Câu 10.
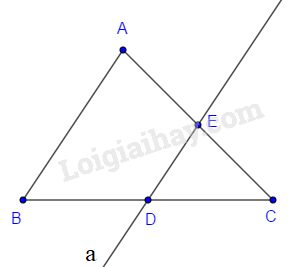
Cho tam giác \(ABC\). Đường thẳng \(a\) cắt \(BC\) ở \(D\). Đường thẳng \(a\) đi qua trung điểm của cạnh \(AC\) nếu
(A) \(BD=DC\)
(B) Đường thẳng \(a\) cắt cạnh \(AC\)
(C) Đường thẳng \(a\) song song với \(AB\)
(D) Có cả hai điều kiện (A) và (C).
Phương pháp giải:
Áp dụng định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
Lời giải chi tiết:
Chọn D.
Câu 11.
Một hình thang có hiệu hai đáy bằng \(4\,cm\), đường trung bình bằng \(5\,cm\). Độ dài của hai đáy bằng
(A) \(8\,cm\) và \(4\,cm\)
(B) \(7\,cm\) và \(3\,cm\)
(C) \(8\,cm\) và \(2\,cm\)
(D) \(4,5\,cm\) và \(0,5\,cm\)
Phương pháp giải:
Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Lời giải chi tiết:
Giả sử độ dài đáy lớn và đáy nhỏ của hình thang lần lượt là \(a;\;b\;(a;b>0)\) \((cm)\)
Hiệu hai đáy bằng \(4\,cm\) nên ta có: \(a-b=4 \Rightarrow a=b+4\) (1)
Đường trung bình hình thang bằng \(5\,cm\) nên ta có:
\((a+b):2=5 \Rightarrow a+b=10\) (2)
Thay (1) và (2) ta được:
\(b+4+b=10\)
\(\eqalign{
& \Rightarrow 2b + 4 = 10 \cr
& \Rightarrow 2b = 10 - 4 \cr
& \Rightarrow b = 6:2 = 3 \cr
& \Rightarrow a = 3 + 4 = 7 \cr} \)
Chọn B.
Câu 12.
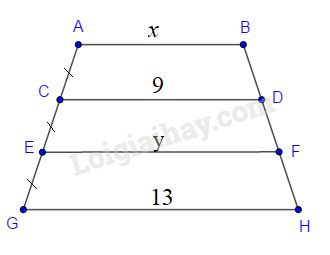
Trên hình 21 ta có \(AB//CD//EF//GH,\) trong đó \(CD=9,\;GH =13.\) Các độ dài \(x\) và \(y\) bằng
(A) \(8\) và \(10\)
(B) \(6\) và \(12\)
(C) \(7\) và \(11\)
(D) \(7\) và \(12\)
Phương pháp giải:
Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
Lời giải chi tiết:
Vì \(AB//EF\) nên \(ABFE\) là hình thang.
Hình thang \(ABFE\) có \(CA=CE\) (gt); \(CB//AB//EF\) (gt) do đó \(CD\) là đường trung bình của hình thang \(ABFE\).
Suy ra:
\(\eqalign{
& CD = \left( {AB + EF} \right):2 = 9 \cr
& \Rightarrow x + y = 9.2 = 18\,\,\,\,\,(1) \cr} \)
Vì \(CD//GH\) nên \(CDHG\) là hình thang.
Hình thang \(CDHG\) có \(EC=EG\) (gt); \(CD//EF//GH\) (gt) do đó \(EF\) là đường trung bình của hình thang \(CDHG\).
Suy ra:
\(\eqalign{
& EF = \left( {CD + GH} \right):2 \cr
& \Rightarrow y = \left( {9 + 13} \right):2 = 11 \cr} \)
Thay\(y=11\) vào (1) ta được: \(x=18-11=7\).
Chọn C.
Loigiaihay.com













Danh sách bình luận