-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 9 TẬP 1
-
CHƯƠNG 1: CĂN BẬC HAI -CĂN BẬC BA
- Bài 1. Căn bậc hai
- Bài 2. Căn thức bậc hai và hằng đẳng thức
- Bài 3. Liên hệ giữa phép nhân và phép khai phương
- Bài 4. Liên hệ giữa phép chia và phép khai phương
- Bài 5. Bảng căn bậc hai
- Bài 6. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Bài 7. Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Bài 8. Rút gọn biểu thức chứa căn thức bậc hai
- Bài 9. Căn bậc ba
- Ôn tập chương 1 - Căn bậc hai. Căn bậc ba
-
CHƯƠNG 2: HÀM SỐ BẬC NHẤT
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 9 TẬP 1
-
CHƯƠNG 1: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- Bài 1. Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Bài 2. Tỉ số lượng giác của góc nhọn
- Bài 3. Bảng lượng giác
- Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn. Thực hành ngoài trời
- Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông
-
CHƯƠNG 2: ĐƯỜNG TRÒN
- Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn
- Bài 2. Đường kính và dây của đường tròn
- Bài 3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
- Bài 4. Vị trí tương đối của đường thẳng và đường tròn
- Bài 5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
- Bài 6. Tính chất của hai tiếp tuyến cắt nhau
- Bài 7. Vị trí tương đối của hai đường tròn
- Ôn tập chương 2 - Đường tròn
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 9 TẬP 2
-
CHƯƠNG 3: HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
-
CHƯƠNG 4: HÀM SỐ y=ax^2 (a khác 0) - PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
- Bài 1. Hàm số y = ax^2 (a ≠ 0)
- Bài 2. Đồ thị của hàm số y=ax^2 (a ≠ 0)
- Bài 3. Phương trình bậc hai một ẩn
- Bài 4. Công thức nghiệm của phương trình bậc hai
- Bài 5. Công thức nghiệm thu gọn
- Bài 6. Hệ thức Vi-ét và ứng dụng
- Bài 7. Phương trình quy về phương trình bậc hai
- Bài 8. Giải bài toán bằng cách lập phương trình
- Ôn tập chương 4 - Hàm số y=ax^2 (a khác 0). Phương trình bậc hai một ẩn
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 9 TẬP 2
-
CHƯƠNG 3: GÓC VỚI ĐƯỜNG TRÒN
- Bài 1. Góc ở tâm. Số đo cung
- Bài 2. Liên hệ giữa cung và dây
- Bài 3. Góc nội tiếp
- Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
- Bài 5. Góc có đỉnh bên trong đường tròn. Góc có đỉnh bên ngoài đường tròn
- Bài 6. Cung chứa góc
- Bài 7. Tứ giác nội tiếp
- Bài 8. Đường tròn ngoại tiếp - Đường tròn nội tiếp
- Bài 9. Độ dài đường tròn, cung tròn
- Bài 10. Diện tích hình tròn, quạt tròn
- Ôn tập chương 3 - Góc với đường tròn
-
CHƯƠNG 4: HÌNH TRỤ - HÌNH NÓN - HÌNH CẦU
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Phần câu hỏi bài 1 trang 84, 85 Vở bài tập toán 9 tập 1
Giải phần câu hỏi bài 1 trang 84, 85 VBT toán 9 tập 1. Hãy khoanh tròn vào chữ cái đứng trước kết quả đúng. Xem hình 18...
Câu 1.
Hãy khoanh tròn vào chữ cái đứng trước kết quả đúng. Xem hình 18.
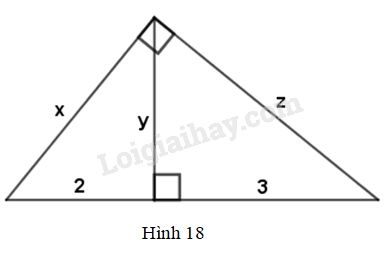
Giá trị của x là:
(A) \(\sqrt 6 \) (B) \(\sqrt {10} \)
(C) \(\sqrt {12} \) (D) \(\sqrt {15} \)
Phương pháp giải:
Áp dụng hệ thức \({a^2} = c.a'\) để tính giá trị của cạnh góc vuông khi biết độ dài cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải chi tiết:
Áp dụng hệ thức \({a^2} = c.a'\) ta có : \({x^2} = \left( {2 + 3} \right).2\) \( \Leftrightarrow {x^2} = 10 \Leftrightarrow x = \sqrt {10} \)
Đáp án cần chọn là B.
Câu 2.
Giá trị của y là:
(A) \(\sqrt 6 \) (B) \(\sqrt {10} \)
(C) \(\sqrt {12} \) (D) \(\sqrt {15} \)
Phương pháp giải:
Áp dụng kiến thức : Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Lời giải chi tiết:
Tam giác vuông có \({h^2} = a'.b'\)
Nên \({y^2} = 2.3 = 6 \Leftrightarrow y = \sqrt 6 \)
Đáp án cần chọn là A.
Câu 3.
Giá trị của z là:
(A) \(\sqrt 6 \) (B) \(\sqrt {10} \)
(C) \(\sqrt {12} \) (D) \(\sqrt {15} \)
Phương pháp giải:
Cách 1: Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Cách 2: Áp dụng định lí Pi-ta-go.
Lời giải chi tiết:
Áp dụng hệ thức \({b^2} = c.b'\) trong tam giác vuông đã cho, ta có:\({z^2} = \left( {2 + 3} \right).3 = 15 \Leftrightarrow z = \sqrt {15} \)
Đáp án cần chọn là D.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1 trang 85 Vở bài tập toán 9 tập 1
- Bài 2 trang 85 Vở bài tập toán 9 tập 1
- Bài 3 trang 86 Vở bài tập toán 9 tập 1
- Bài 4 trang 86 Vở bài tập toán 9 tập 1
- Bài 5 trang 86 Vở bài tập toán 9 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
