-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ - SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Lũy thừa của một số hữu tỉ
- Bài 6. Lũy thừa của một số hữu tỉ ( tiếp theo)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ - Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơclit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC . CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Ôn tập chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 64 trang 103 Vở bài tập toán 7 tập 2
Giải bài 64 trang 103, 104 VBT toán 7 tập 2. Cho tam giác MNP với đường trung tuyến MR và trọng tâm Q...
Đề bài
Cho tam giác \(MNP\) với đường trung tuyến \(MR\) và trọng tâm \(Q.\)
a) Tính tỉ số các diện tích của hai tam giác \(MPQ\) và \(RPQ.\)
b) Tính tỉ số các diện tích của hai tam giác \(MNQ\) và \(RNQ.\)
Từ các kết quả trên, hãy chứng minh các tam giác \(QMN, QNP, QPM\) có cùng diện tích.
Gợi ý: Hai tam giác ở mỗi câu a, b, c có chung chiều cao.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất trọng tâm của tam giác.
Lời giải chi tiết
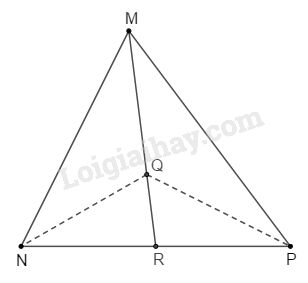
a) Theo tính chất trọng tâm của tam giác, ta có \(MQ = 2QR.\)
Hai tam giác \(MPQ\) và \(RPQ\) có đáy \(MQ=2QR\) và có chung chiều cao kẻ từ \(P\) xuống \(MQ\) nên \( S_{MPQ}= 2S_{ RPQ}\) (1), hay \(\dfrac{S_{MPQ}}{S_{RPQ}} = 2 \)
b) Hai tam giác \(MNQ\) và \(RNQ\) có đáy \(MQ=2QR\) và có chung chiều cao kẻ từ \(N\) xuống \(MR\) nên \( S_{MNQ}= 2S_{ RNQ}\) (2), hay \(\dfrac{S_{MNQ}}{S_{RNQ}} = 2 \)
c) Hai tam giác \(RPQ\) và \(RNQ\) có đáy \(NR=RP\) (giả thiết) và có chung chiều cao kẻ từ \(Q\) xuống \(PN\) nên \({S_{RPQ}} = {S_{RQN}}\)
\({S_{QNP}} = {S_{RPQ}} + {S_{RQN}}= 2{S_{RPQ}} \)\(\,= 2{S_{RQN}}\) (3)
Từ (1), (2) và (3) suy ra \({S_{QMN}} ={S_{QNP}} ={S_{MPQ}}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 65 trang 104 Vở bài tập toán 7 tập 2
- Bài 66 trang 105 Vở bài tập toán 7 tập 2
- Bài 67 trang 105 Vở bài tập toán 7 tập 2
- Đề kiểm tra 45 phút chương 3 phần Hình học 7 - Đề số 1
- Đề kiểm tra 45 phút chương 3 phần Hình học 7 - Đề số 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
