-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ - SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Lũy thừa của một số hữu tỉ
- Bài 6. Lũy thừa của một số hữu tỉ ( tiếp theo)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ - Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơclit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC . CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Ôn tập chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 54 trang 97 Vở bài tập toán 7 tập 2
Giải bài 54 trang 97 VBT toán 7 tập 2. Chứng minh rằng trong một tam giác cân, đường cao xuất phát từ đỉnh đối diện với đáy đồng thời là đường phân giác cùng xuất phát từ đỉnh này...
Đề bài
Chứng minh rằng trong một tam giác cân, đường cao xuất phát từ đỉnh đối diện với đáy đồng thời là đường phân giác cùng xuất phát từ đỉnh này.
Phương pháp giải - Xem chi tiết
Chứng minh tam giác \(ABH\) và tam giác \(ACH\) có \(\widehat {BAH} = \widehat {CAH}\).
Lời giải chi tiết
\(\begin{array}{l}
GT:\,\Delta ABC,AB = AC,AH \bot BC\,tại\,H\\
KL:\,\widehat {BAH} = \widehat {CAH}
\end{array}\)
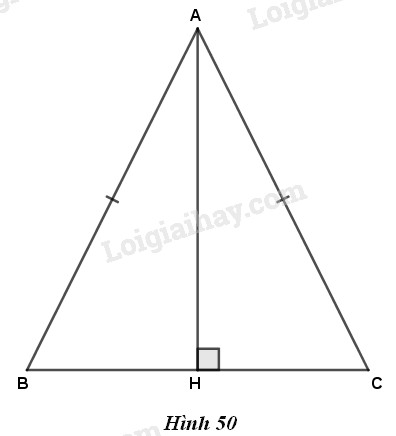
Giả sử tam giác \(ABC\) cân tại \(A\) và \(AH\) là một đường cao của nó. Ta sẽ chứng minh \(\widehat {BAH} = \widehat {CAH}\).
Xét hai tam giác vuông \(ABH\) và \(CAH\).
Ta có \(AB=AC\), cạnh \(AH\) chung.
Vậy \(\Delta ABH = \Delta CAH\) (cạnh huyền - cạnh góc vuông). Suy ra \(\widehat {BAH} = \widehat {CAH}\), do đó \(AH\) là đường phân giác của góc \(BAC\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 55 trang 98 Vở bài tập toán 7 tập 2
- Bài 56 trang 98 Vở bài tập toán 7 tập 2
- Bài 57 trang 99 Vở bài tập toán 7 tập 2
- Bài 58 trang 99 Vở bài tập toán 7 tập 2
- Bài 59 trang 100 Vở bài tập toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
