Bài 8. Đối xứng tâm

Bài 38 trang 120 Vở bài tập toán 8 tập 1

Giải bài 38 trang 120 VBT toán 8 tập 1. Cho hình bình hành ABCD, O là giao điểm của hai đường chéo...

Đề bài

Cho hình bình hành \(ABCD\), \(O\) là giao điểm của hai đường chéo. Một đường thẳng đi qua \(O\) cắt các cạnh \(AB\) và \(CD\) theo thứ tự ở \(M\) và \(N\). Chứng minh rằng điểm \(M\) đối xứng với điểm \(N\) qua \(O\).

Phương pháp giải - Xem chi tiết

Áp dụng:

+) Hình bình hành có các cạnh đối song song.

+) Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.

Lời giải chi tiết

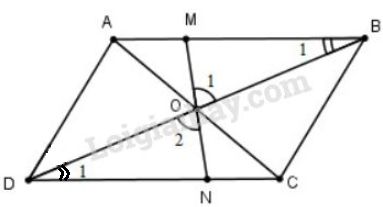
\(\Delta BOM\) và \(\Delta DON\) có:

\(\widehat{B_{1}} = \widehat{D_{1}}\) (so le trong, \(AB//DC\))

\(OB = OD\) (tính chất đường chéo hình bình hành)

\(\widehat{O_{1}} = \widehat{O_{2}}\) (đối đỉnh)

Do đó \( ∆BOM = ∆DON (g.c.g)\) suy ra \(OM = ON\). \(O\) là trung điểm của \(MN\) nên \(M \) đối xứng với \(N\) qua \(O\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 10 phiếu

Bài tiếp theo

Bài 37 trang 119 Vở bài tập toán 8 tập 1
Giải bài 37 trang 119 VBT toán 8 tập 1. Cho góc vuông xOy, điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua Ox, gọi C là điểm đối xứng với A qua Oy...
Bài 36 trang 119 Vở bài tập toán 8 tập 1
Giải bài 36 trang 119 VBT toán 8 tập 1. Cho hình 50, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với điểm M qua điểm I.
Bài 35 trang 118 Vở bài tập toán 8 tập 1
Giải bài 35 trang 118 VBT toán 8 tập 1. Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C...
Bài 34 trang 118 Vở bài tập toán 8 tập 1
Giải bài 34 trang 118 VBT toán 8 tập 1. Trong mặt phẳng tọa độ, cho điểm H có tọa độ (3; 2). Hãy vẽ điểm K đối xứng với H qua gốc tọa độ và tìm tọa độ K.
Phần câu hỏi bài 8 trang 117, 118 Vở bài tập toán 8 tập 1
Giải phần câu hỏi bài 8 trang 117, 118 VBT toán 8 tập 1. Hai điểm A và B đối xứng với nhau qua điểm C nếu...