Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đ..

Bài 1 trang 111 Vở bài tập toán 9 tập 1

Giải bài 1 trang 111 VBT toán 9 tập 1. Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm...

Đề bài

Cho hình chữ nhật ABCD có \(AB = 12cm, BC = 5cm.\) Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn, tính bán kính của đường tròn đó.

Phương pháp giải - Xem chi tiết

Tìm điểm cách đều bốn đỉnh \(A,B,C,D\) rồi tìm bán kính của đường tròn.

Lời giải chi tiết

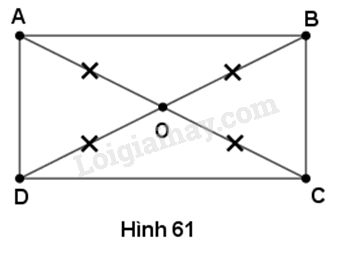
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)

Ta có \(OA = OC = \dfrac{1}{2}AC\)

\(OB = OA\)

\(AC = BD\) (tính chất đường chéo hình chữ nhật).

Nên \(OA = OB = OC = OD\)

Các điểm \(A,B,C,D\) cách đều điểm\(O\) nên cùng thuộc đường tròn tâm \(O\) bán kính \(AO.\)

Áp dụng định lí Pi-ta-go vào tam giác \(ABC\) vuông tại \(B,\) ta có :

\(A{C^2} = A{B^2} + B{C^2} = {12^2} + {5^2} \)\(= 144 + 25 = 169,\) suy ra \(AC=13\)

Bán kính của đường tròn bằng \(\dfrac{{AC}}{2} \)\(= \dfrac{{13}}{2} = 6,5\left( {cm} \right).\)

Loigiaihay.com

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Các bài liên quan: - Bài 1. Sự xác định đường tròn. Tính chất đối xứng của đường tròn

Báo lỗi - Góp ý Gửi góp ý ngay, nhận quà liền tay!

>> Học trực tuyến lớp 9 và luyện vào lớp 10 tại Tuyensinh247.com. , cam kết giúp học sinh lớp 9 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục