 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Đề ôn tập học kì 2 – Có đáp án và lời giải
Đề ôn tập học kì 2 – Có đáp án và lời giải
Đề số 7 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12
Đáp án và lời giải chi tiết Đề số 7 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán học 12
Đề bài
Câu 1: Trong không gian Oxyz, cho hai điểm \(M\left( {2;1; - 2} \right);N\left( {4; - 5;1} \right)\). Độ dài đoạn thẳng MN bằng
A. \(\sqrt {41} \) B. 7.
C. 49. D. \(\sqrt 7 \)
Câu 2: Họ các nguyên hàm của hàm số \(f\left( x \right) = {\left( {2x + 3} \right)^5}\) là
A. \(F\left( x \right) = 10{\left( {2x + 3} \right)^4} + C.\)
B. \(F\left( x \right) = 5{\left( {2x + 3} \right)^4} + C.\)
C. \(F\left( x \right) = \frac{{{{\left( {2x + 3} \right)}^6}}}{{12}} + C.\)
D. \(F\left( x \right) = \frac{{{{\left( {2x + 3} \right)}^6}}}{6} + C.\)
Câu 3: Cho số phức \(z = 2 - i\). Trong mặt phẳng tọa độ Oxyz, điểm biểu diễn của số phức \(\overline z \) có tọa độ là
A. \(\left( {2; - 1} \right).\) B. \(\left( {2;1} \right).\)
C. \(\left( {1;2} \right).\) D. \(\left( { - 2;1} \right).\)
Câu 4: Số phức z thỏa mãn \(2z - 3\left( {1 + i} \right) = iz + 7 - 3i\) là
A. \(z = \frac{{14}}{5} + \frac{8}{5}i.\)
B. \(z = 4 - 2i.\)
C. \(z = 4 + 2i.\)
D. \(z = \frac{{14}}{5} - \frac{8}{5}i.\)
Câu 5: Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng
A. \(\int\limits_a^b {\left| {f\left( x \right) + g\left( x \right)} \right|dx} \)
B. \(\int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
C. \(\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \)
D. \(\left| {\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} } \right|.\)
Câu 6: Tích phân \(\int\limits_1^e {\frac{{\ln x}}{x}dx} \) bằng:
A. \(\frac{{{e^2} + 1}}{2}\)
B. \(\frac{1}{2}\)
C. \( - \frac{1}{2}\)
D. \(\frac{{{e^2} - 1}}{2}\)
Câu 7: Trong không gian Oxyz, phương trình mặt cầu có tâm \(I\left( { - 1;1; - 2} \right)\) và đi qua điểm \(A\left( {2;1;2} \right)\) là
A. \({\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 25.\)
B. \({\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 5.\)
C. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 25.\)
D. \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 2} \right)^2} = 25.\)
Câu 8: Tích phân \(\int\limits_0^1 {\left( {3x + 1} \right)\left( {x + 3} \right)dx} \) bằng
A. 6. B. 12.
C. 9. D. 5.
Câu 9: Trong không gian Oxyz, mặt phẳng \(\left( P \right):2x - z + 1 = 0\) có một vecto pháp tuyến là
A. \(\overrightarrow n = \left( {2; - 1;1} \right)\).
B. \(\overrightarrow n = \left( {2;0; - 1} \right)\)
C. \(\overrightarrow n = \left( {2;0;1} \right)\)
D. \(\overrightarrow n = \left( {2;1; - 1} \right)\)
Câu 10: Diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y = {\left( {x - 2} \right)^2} - 1\), trục hoành và hai đường thẳng \(x = 1;\) \(x = 2\) bằng
A. \(\frac{7}{3}.\) B. \(\frac{2}{3}.\)
C. \(\frac{3}{2}.\) D. \(\frac{1}{3}.\)
Câu 11: Biết rằng \(\left( {2 + 3i} \right)a + \left( {1 - 2i} \right)b = 4 + 13i\) với \(a,\,\,b\) là các số thực. Giá trị của \(a + b\) bằng
A. 1. B. 9.
C. 5. D. \( - 3.\)
Câu 12: Giá trị dương của tham số m sao cho diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x + 3\) và các đường thẳng \(y = 0,\) \(x = 0,\) \(x = m\) bằng 10 là
A. \(m = 5\) B. \(m = 1.\)
C. \(m = \frac{7}{2}.\) D. \(m = 2.\)
Câu 13: Trong không gian Oxyz, cho hai điểm \(A\left( {1;3;5} \right)\) và \(B\left( {1; - 1;1} \right)\). Trung điểm của đoạn thẳng AB có tọa độ là
A. \(\left( {2;2;6} \right)\)
B. \(\left( {0; - 4; - 4} \right)\)
C. \(\left( {0; - 2; - 2} \right)\)
D. \(\left( {1;1;3} \right)\)
Câu 14: Hai số phức \(\frac{3}{2} + \frac{{\sqrt 7 }}{2}i\) và \(\frac{3}{2} - \frac{{\sqrt 7 }}{2}i\) là nghiệm của phương trình nào sau đây?
A. \({z^2} - 3z - 4 = 0\)
B. \({z^2} + 3z + 4 = 0\)
C. \({z^2} - 3z + 4 = 0\)
D. \({z^2} + 3z - 4 = 0\)
Câu 15: Họ nguyên hàm của hàm số \(f\left( x \right) = \sin 2x\) là
A. \(F\left( x \right) = - \frac{1}{2}\cos 2x + C.\)
B. \(F\left( x \right) = - \cos 2x + C.\)
C. \(F\left( x \right) = - 2\cos 2x + C.\)
D. \(F\left( x \right) = \frac{1}{2}\cos 2x + C.\)
Câu 16: Trong không gian Oxyz, phương trình tham số của đường thẳng đi qua điểm \(M\left( {2;0; - 1} \right)\) và có vecto chỉ phương \(\overrightarrow a = \left( {2; - 3;1} \right)\) là
A. \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3t\\z = - 1 + t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 6\\z = 2 - t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 3t\\z = 2 - t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = - 2 + 4t\\y = - 6t\\z = 1 + 2t\end{array} \right.\)
Câu 17: Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 2x\), trục hoành, đường thẳng \(x = 0;\) \(x = 1\) quanh trục hoành bằng
A. \(\frac{{2\pi }}{3}.\) B. \(\frac{{4\pi }}{3}.\)
C. \(\frac{{8\pi }}{{15}}.\) D. \(\frac{{16\pi }}{{15}}.\)
Câu 18: Cho hàm số \(f\left( x \right)\) liên tục có đạo hàm trên đoạn \(\left[ { - 1;2} \right],\) \(f\left( { - 1} \right) = 8;\) \(f\left( 2 \right) = - 1\). Tích phân \(\int\limits_{ - 1}^2 {f'\left( x \right)dx} \) bằng
A. \( - 9\) B. 9.
C. 1. D. 7.
Câu 19: Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):\,\,x + 2y - 2z - 2 = 0\) và điểm \(I\left( {1;2; - 3} \right)\). Bán kính của mặt cầu có tâm \(I\) và tiếp xúc với mặt phẳng \(\left( P \right)\) bằng:
A. \(1\) B. \(\frac{{11}}{3}\)
C. \(3\) D. \(\frac{1}{3}\)
Câu 20: Trong không gian Oxyz, mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\) có tọa độ tâm I và bán kính R lần lượt là
A. \(I\left( { - 4;1;0} \right);\,\,R = 4.\)
B. \(I\left( {8; - 2;0} \right);\,\,R = 2\sqrt 7 .\)
C. \(I\left( {4; - 1;0} \right);\,\,R = 4.\)
D. \(I\left( {4; - 1;0} \right);\,\,R = 16.\)
Câu 21: Trong không gian Oxyz, cho điểm \(I\left( {1;2;0} \right)\) và mặt phẳng \(\left( P \right):2x - 2y + z - 7 = 0\). Gọi \(\left( S \right)\) là mặt cầu có tâm I và cắt mặt phẳng \(\left( P \right)\) theo giao tuyến là một đường tròn \(\left( C \right)\). Biết rằng hình tròn \(\left( C \right)\) có diện tích bằng \(16\pi \). Mặt cầu \(\left( S \right)\) có phương trình là
A. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 16.\)
B. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 7.\)
C. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 25.\)
D. \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 9.\)
Câu 22: Tích phân \(\int\limits_0^1 {\left( {x - 2} \right){e^{2x}}dx} \) bằng
A. \(\frac{{5 - 3{e^2}}}{4}.\)
B. \(\frac{{5 - 3{e^2}}}{2}.\)
C. \(\frac{{5 + 3{e^2}}}{4}.\)
D. \(\frac{{ - 5 - 3{e^2}}}{4}.\)
Câu 23: Họ nguyên hàm của hàm số \(f\left( x \right) = x\sin x\) là
A. \(F\left( x \right) = x\cos x + \sin x + C.\)
B. \(F\left( x \right) = x\cos x - \sin x + C.\)
C. \(F\left( x \right) = - x\cos x - \sin x + C.\)
D. \(F\left( x \right) = - x\cos x + \sin x + C.\)
Câu 24: Diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 4x - {x^2}\) và \(y = 2x\) bằng
A. \(\frac{{20}}{3}.\) B. \(\frac{{16}}{3}\)
C. 4. D. \(\frac{4}{3}\)
Câu 25: Cho \(\int {f\left( x \right)dx = F\left( x \right) + C} \). Khi đó \(\int {f\left( {2x - 3} \right)dx} \)
A. \(F\left( {2x - 3} \right) + C.\)
B. \(\frac{1}{2}F\left( {2x - 3} \right) + C.\)
C. \(\frac{1}{2}F\left( {2x} \right) - 3 + C.\)
D. \(F\left( {2x} \right) - 3 + C.\)
Câu 26: Gọi \({z_1};\,\,{z_2}\) lần lượt là nghiệm của phương trình \({z^2} - 2z + 5 = 0\). Giá trị \({\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\) bằng
A. 10. B. \(2\sqrt 5 \)
C. 2. D. 20.
Câu 27: Trong không gian Oxyz, phương trình của mặt phẳng đi qua điểm \(M\left( {2; - 3;4} \right)\) và có vecto pháp tuyến \(\overrightarrow n = \left( { - 2;4;1} \right)\) là
A. \(2x - 4y - z - 12 = 0.\)
B. \(2x - 3y + 4z - 12 = 0\)
C. \(2x - 4y - z + 12 = 0\)
D. \(2x - 3y + 4z + 12 = 0\)
Câu 28: Phần ảo của số phức\(z = 2019 + {i^{2019}}\) bằng
A. 2019 B. -1
C. -2019 D. 1
Câu 29: Mô đun của số phức \(z = - 1 + i\) bằng
A. 2. B. 1.
C. 0. D. \(\sqrt 2 .\)
Câu 30: Tìm số phức z thỏa mãn \(\overline z = 2 - i\) là
A. \(z = 2 + i\).
B. \(z = 1 - 2i\)
C. \(z = - 2 - i\)
D. \(z = - 2 + i\)
Câu 31: Biết số phức thỏa mãn \(\left| {iz - 3} \right| = \left| {z - 2 - i} \right|\) và \(\left| z \right|\) có giá trị nhỏ nhất. Phần thực của số phức z bằng
A. \(\frac{2}{5}.\) B. \(\frac{1}{5}.\)
C. \( - \frac{2}{5}.\) D. \( - \frac{1}{5}.\)
Câu 32: Biết \(F\left( x \right) = - \frac{{\left( {x - a} \right){\rm{cos3}}x}}{b} + \frac{1}{c}\sin 3x + 2019\) là một nguyên hàm của hàm số \(f\left( x \right) = \left( {x - 2} \right)\sin 3x,\)\(a,\,\,b,\,\,c \in \mathbb{Z}\) . Giá trị của \(ab + c\) bằng
A. 18. B. 14.
C. 15. D. 10.
Câu 33: Trong không gian Oxyz, cho hai vecto \(\overrightarrow m = \left( {4;3;1} \right)\) và \(\overrightarrow n = \left( {0;0;1} \right)\). Gọi \(\overrightarrow p \) là vecto cùng hướng với \(\left[ {\overrightarrow m ;\overrightarrow n } \right]\) và \(\left| {\overrightarrow p } \right| = 15\). Tìm tọa độ của \(\overrightarrow p \) là
A. \(\left( { - 9;12;0} \right)\)
B. \(\left( {9; - 12;0} \right)\)
C. \(\left( {0;9; - 12} \right)\)
D. \(\left( {0; - 9;12} \right)\)
Câu 34: Trong không gian Oxyz cho hình thang cân ABCD có đáy AB và CD. Biết \(A\left( {3;1; - 2} \right),\) \(B\left( { - 1;3;2} \right),\) \(C\left( { - 6;3;6} \right);\) \(D\left( {a;b;c} \right);\) \(a,b,c \in \mathbb{R}\). Giá trị \(a + b + c\) bằng
A. \( - 1\). B. 1.
C. 3. D. \( - 3.\)
Câu 35: Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ dưới. mệnh đề nào sau đây là đúng?
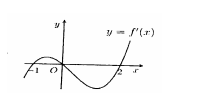
A. \(f\left( 0 \right) > f\left( 2 \right) > f\left( { - 1} \right).\)
B. \(f\left( 0 \right) > f\left( { - 1} \right) > f\left( 2 \right).\)
C. \(f\left( 2 \right) > f\left( 0 \right) > f\left( { - 1} \right).\)
D. \(f\left( { - 1} \right) > f\left( 0 \right) > f\left( 2 \right).\)
Câu 36: Cho số phức \(z = m - 2 + \left( {{m^2} - 1} \right)i,\,\,m \in \mathbb{R}\). Gọi \(\left( C \right)\) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và trục hoành bằng
A. \(\frac{4}{3}.\) B. \(\frac{{32}}{3}.\)
C. \(\frac{8}{3}.\) D. 1.
Câu 37: Hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong \(\left( C \right)\) có phương trình \(y = \frac{1}{4}{x^2}\). Gọi \({S_1};\,\,{S_2}\) lần lượt là diện tích phần không bị gạch và phần bị gạch như hình bên dưới. Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng.
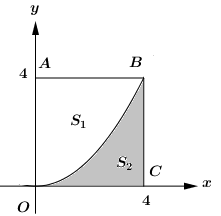
A. \(\frac{3}{2}.\) B. 3.
C. \(\frac{1}{2}.\) D. 2.
Câu 38: Biết tích phân \(\int\limits_0^{\frac{\pi }{6}} {\frac{{dx}}{{1 + \sin x}} = \frac{{a\sqrt 3 + b}}{c}} \)\(;a,\,\,b,\,\,c\) là các số nguyên. Giá trị \(a + b + c\) bằng
A. \( - 1.\) B. 12.
C. 7. D. 5.
Câu 39: Trong không gian Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 4x - 6y + m = 0\) với m là tham số; và đường thằng \(\Delta :\left\{ \begin{array}{l}x = 4 + 2t\\y = 3 + t\\z = 3 + 2t\end{array} \right.\). Biết đường thẳng \(\Delta \) cắt mặt cầu \(\left( S \right)\) tại hai điểm phân biệt A ,B sao cho \(AB = 8\). Giá trị của m là
A. \(m = 12.\)
B. \(m = - 12.\)
C. \(m = - 10.\)
D. \(m = 5.\)
Câu 40: Một ô tô đang chạy với vận tốc 20 m/s thì người ta nhìn thấy một chướng ngại vật nên đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc \(v\left( t \right) = - 2t + 20\), trong đó t là thời gian (tính bằng giấy) kể từ lúc đạp phanh. Quãng đường mà ô tô đi được trong 15 giây cuối cùng bằng
A. 125 m. B. 75 m.
C. 200 m. D. 100 m.
Câu 41: Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):2x - y + 2z + 1 = 0\) và hai điểm \(A\left( {1;0; - 2} \right),\) \(B\left( { - 1; - 1;3} \right)\). Mặt phẳng \(\left( Q \right)\) đi qua hai điểm A, B và vuông góc với mặt phẳng \(\left( P \right)\) có phương trình là
A. \(3x + 14y + 4z - 5 = 0.\)
B. \(2x - y + 2z - 2 = 0.\)
C. \(2x - y + 2z + 2 = 0.\)
D. \(3x + 14y + 4z + 5 = 0.\)
Câu 42: Cho hàm số \(f\left( x \right)\) liên tục, có đạo hàm trên \(\mathbb{R}\), \(f\left( 2 \right) = 16\) và \(\int\limits_0^8 {f\left( x \right)dx = 4} \). Tích phân \(\int\limits_0^4 {xf'\left( {\frac{x}{2}} \right)dx} \) bằng:
A. 112. B. 12.
C. 56. D. 144.
Câu 43: Biết rằng \(\int\limits_0^1 {x{e^{{x^2} + 2}}dx = \frac{a}{2}\left( {{e^b} - {e^c}} \right)} \) với \(a,\,\,b,\,\,c \in \mathbb{Z}\). Giá trị của \(a + b + c\) bằng
A. 4. B. 7.
C. 5. D. 6.
Câu 44: Biết rằng \(z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\) \(\left( {m \in \mathbb{R}} \right)\) là một số thực. Giá trị của biểu thức \(1 + z + {z^2} + {z^3} + ... + {z^{2019}}\) bằng
A. 2019. B. 0.
C. 1. D. 2020.
Câu 45: Trong không gian Oxyz, cho đường thẳng \({d_1}:\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 2}} = \frac{{z - 3}}{1}\) và điểm \(A\left( {1;0; - 1} \right)\). Gọi \({d_2}\) là đường thẳng đi qua A và có vecto chỉ phương \(\overrightarrow u = \left( {a;1;2} \right)\). Giá trị của a sao cho đường thẳng \({d_1}\) cắt đường thẳng \({d_2}\) là
A. \(a = - 1.\)
B. \(a = 2.\)
C. \(a = 0.\)
D. \(a = 1.\)
Câu 46: Trong không gian Oxyz, cho hai điểm \(A\left( {3;5; - 1} \right)\) và \(B\left( {1;1;3} \right)\). Tọa độ điểm M thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) nhỏ nhất là
A. \(M\left( { - 2;3;0} \right).\)
B. \(M\left( {2;3;0} \right).\)
C. \(M\left( { - 2; - 3;0} \right).\)
D. \(M\left( {2; - 3;0} \right).\)
Câu 47: Trong không gian Oxyz, biết mặt cầu \(\left( S \right)\) tâm O và tiếp xúc với mặt phẳng \(\left( P \right):x - 2y + 2z + 9 = 0\) tại điểm \(H\left( {a;b;c} \right)\). Giá trị tổng \(a + b + c\) bằng
A. 2. B. \( - 1.\)
C. 1. D. \( - 2.\)
Câu 48: Trong không gian Oxyz, cho đường thẳng \(d:\frac{x}{2} = \frac{{y - 3}}{1} = \frac{{z - 2}}{{ - 3}}\) và mặt phẳng \(\left( P \right):x - y + 2z - 6 = 0\). Đường thẳng nằm trong mặt phẳng \(\left( P \right)\), cắt và vuông góc với đường thẳng d có phương trình là
A. \(\frac{{x + 2}}{1} = \frac{{y - 2}}{7} = \frac{{z - 5}}{3}.\)
B. \(\frac{{x - 2}}{1} = \frac{{y - 4}}{7} = \frac{{z + 1}}{3}.\)
C. \(\frac{{x + 2}}{1} = \frac{{y + 4}}{7} = \frac{{z - 1}}{3}.\)
D. \(\frac{{x - 2}}{1} = \frac{{y + 2}}{7} = \frac{{z + 5}}{3}.\)
Câu 49: Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = {x^2} + x\) và \(F\left( 1 \right) = 1\). Giá trị của \(F\left( { - 1} \right)\) bằng
A. \(\frac{1}{3}.\) B. 1.
C. \(\frac{1}{2}.\) D. \(\frac{1}{6}.\)
Câu 50: Biết số phức z thỏa mãn điều kiện \(\frac{{5\left( {\overline z + i} \right)}}{{z + 1}} = 2 - i\). Mô đun số phức \({\rm{w}} = 1 + z + {z^2}\) bằng
A. 13. B. 2.
C. \(\sqrt {13} .\) D. \(\sqrt 2 \)
Lời giải chi tiết
|
1. B |
2. C |
3. B |
4. C |
5. B |
|
6. B |
7. A |
8. C |
9. B |
10. B |
|
11. A |
12. D |
13. D |
14. C |
15. A |
|
16. A |
17. C |
18. A |
19. C |
20. A |
|
21. C |
22. A |
23. D |
24. D |
25. B |
|
26. A |
27. A |
28. B |
29. D |
30. A |
|
31. D |
32. C |
33. B |
34. D |
35. B |
|
36. A |
37. D |
38. D |
39. B |
40. B |
|
41. D |
42. A |
43. D |
44. D |
45. C |
|
46. B |
47. B |
48. A |
49. A |
50. C |
Câu 1 (NB)
Phương pháp:
Áp dụng công thức tính độ dài đoạn thẳng: \(MN = \) \(\sqrt {{{\left( {{x_N} - {x_M}} \right)}^2} + {{\left( {{y_N} - {y_M}} \right)}^2} + {{\left( {{z_N} - {z_M}} \right)}^2}} \)
Cách giải:
\(MN = \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( { - 5 - 1} \right)}^2} + {{\left( {1 + 2} \right)}^2}} \)\( = 7\)
Chọn B.
Câu 2 (TH)
Phương pháp:
Áp dụng công thức tính nguyên hàm của hàm số mũ: \(\int {{{\left( {ax + b} \right)}^c}dx = \frac{1}{a}\frac{{{{\left( {ax + b} \right)}^{c + 1}}}}{{c + 1}}} \)
Cách giải:
Ta có \(\int {{{\left( {2x + 3} \right)}^5}dx = \frac{1}{2}.\frac{{{{\left( {2x + 3} \right)}^6}}}{6} + C} \)\( = \frac{{{{\left( {2x + 3} \right)}^6}}}{{12}} + C\)
Chọn C.
Câu 3 (NB)
Phương pháp:
- Số phức liên hợp của số phức \(z = a + bi\) là \(\overline z = a - bi\).
- Điểm biểu diễn số phức \(\overline z = a - bi\) trong mặt phẳng tọa độ là \(M\left( {a; - b} \right)\).
Cách giải:
Ta có: \(z = 2 - i \Rightarrow \overline z = 2 + i\)
\( \Rightarrow \) Điểm biểu diễn của số phức \(\overline z \) trong mặt phẳng tọa độ là \(\left( {2;1} \right).\)
Chọn B.
Câu 4 (TH)
Phương pháp:
Đưa phương trình về phương trình bậc nhất đối với \(z\) và tìm \(z\).
Cách giải:
\(\begin{array}{l}2z - 3\left( {1 + i} \right) = iz + 7 - 3i\\ \Leftrightarrow \left( {2 - i} \right)z = 7 - 3i + 3\left( {1 + i} \right)\\ \Leftrightarrow \left( {2 - i} \right)z = 10\\ \Leftrightarrow z = \frac{{10}}{{2 - i}} = 4 + 2i\end{array}\)
Chọn C.
Câu 5 (NB)
Phương pháp:
Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Cách giải:
Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Chọn B.
Câu 6 (TH)
Phương pháp:
Sử dụng phương pháp tính phân từng phần: \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \).
Cách giải:
Ta có \(I = \int\limits_1^e {\frac{{\ln x}}{x}dx} \)
Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = \frac{{dx}}{x}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{x}\\v = \ln x\end{array} \right.\)
Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,I = \left. {{{\ln }^2}x} \right|_1^e - \int\limits_1^e {\frac{{\ln x}}{x}dx} \\ \Leftrightarrow I = {\ln ^2}e - {\ln ^2}1 - I\\ \Leftrightarrow 2I = 1 \Leftrightarrow I = \frac{1}{2}\end{array}\)
Chọn B.
Câu 7 (TH)
Phương pháp:
- Mặt cầu tâm \(I\) đi qua điểm \(A\) có bán kính \(R = IA\).
- Sử dụng công thức tính độ dài đoạn thẳng:
\(IA = \)\(\sqrt {{{\left( {{x_A} - {x_I}} \right)}^2} + {{\left( {{y_A} - {y_I}} \right)}^2} + {{\left( {{z_A} - {z_I}} \right)}^2}} \)
- Viết phương trình mặt cầu khi biết tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Cách giải:
Ta có \(I\left( { - 1;1; - 2} \right);A\left( {2;1;2} \right)\) \( \Rightarrow IA = \sqrt {{3^2} + {0^2} + {4^2}} = 5\)
Vì mặt cầu tâm \(I\) đi qua điểm \(A\) có bán kính \(R = IA = 5\).
Vậy phương trình mặt cầu cần tìm là: \({\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 2} \right)^2} = 25.\)
Chọn A.
Câu 8 (NB)
Phương pháp:
- Nhân phá ngoặc biểu thức dưới dấu tích phân.
- Sử dụng nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\,\,\left( {n \ne - 1} \right)\).
Cách giải:
\(\begin{array}{l}\,\,\,\,\int\limits_0^1 {\left( {3x + 1} \right)\left( {x + 3} \right)dx} \\ = \int\limits_0^1 {\left( {3{x^2} + 10x + 3} \right)dx} \\ = \left. {\left( {{x^3} + 5{x^2} + 3x} \right)} \right|_0^1 = 9\end{array}\)
Chọn C.
Câu 9 (NB)
Phương pháp:
Mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\).
Cách giải:
Mặt phẳng \(\left( P \right):2x - z + 1 = 0\) có 1 vecto pháp tuyến là \(\left( {2;0; - 1} \right).\)
Chọn B.
Câu 10 (TH)
Phương pháp:
- Giải phương trình hoành độ giao điểm tìm các nghiệm thuộc \(\left[ {1;2} \right]\).
- Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Cách giải:
Xét phương trình hoành độ giao điểm: \({\left( {x - 2} \right)^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 2 = - 1\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\left( {x - 2} \right)^2} - 1\), trục hoành và hai đường thẳng \(x = 1,x = 2\) bằng: \(S = \int\limits_1^2 {\left| {{{\left( {x - 2} \right)}^2} - 1} \right|dx} \)\( = \int\limits_1^2 {\left( { - {x^2} + 4x - 3} \right)dx} = \frac{2}{3}.\)
Chọn B.
Câu 11 (TH)
Phương pháp:
- Hai số phức bằng nhau \({a_1} + {b_1}i = {a_2} + {b_2}i \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} = {b_2}\end{array} \right.\).
- Giải hệ phương trình tìm \(a,\,\,b\) sau đó tính tổng \(a + b\).
Cách giải:
\(\begin{array}{l}\,\,\,\,\,\,\left( {2 + 3i} \right)a + \left( {1 - 2i} \right)b = 4 + 13i\\ \Leftrightarrow \left( {2a + b} \right) + \left( {3a - 2b} \right)i = 4 + 13i\\ \Leftrightarrow \left\{ \begin{array}{l}2a + b = 4\\3a - 2b = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 2\end{array} \right.\end{array}\)
Vậy \(a + b = 3 + \left( { - 2} \right) = 1.\)
Chọn A.
Câu 12 (TH)
Phương pháp:
Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Cách giải:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = 2x + 3\) và các đường thẳng \(y = 0,\) \(x = 0,\) \(x = m\) bằng là: \(S = \int\limits_0^m {\left| {2x + 3} \right|dx} \)\( = \left| {\left. {\left( {{x^2} + 3x} \right)} \right|_0^m} \right| = \left| {{m^2} + 3m} \right|.\)
Theo bài ra ta có: \(S = 10\)
\(\begin{array}{l} \Leftrightarrow \left| {{m^2} + 3m} \right| = 10\\ \Leftrightarrow \left[ \begin{array}{l}{m^2} + 3m = 10\\{m^2} + 3m = - 10\,\,\left( {VN} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 5\end{array} \right.\end{array}\)
Mà \(m\) là số nguyên dương. Vậy \(m = 2\).
Chọn D.
Câu 13 (NB)
Phương pháp:
Điểm \(I\) là trung điểm của \(AB\) thì \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\\{z_I} = \frac{{{z_A} + {z_B}}}{2}\end{array} \right.\).
Cách giải:
Gọi \(I\) là trung điểm của \(AB\)\( \Rightarrow I\left( {\frac{{1 + 1}}{2};\frac{{3 + \left( { - 1} \right)}}{2};\frac{{5 + 1}}{2}} \right)\)\( \Rightarrow I\left( {1;1;3} \right).\)
Chọn D.
Câu 14 (TH)
Phương pháp:
- Tính tổng \(S = {z_1} + {z_2}\) và tích \(P = {z_1}{z_2}\) của hai số phức.
- Khi đó \({z_1},\,\,{z_2}\) là hai nghiệm của phương trình \({X^2} - SX + P = 0.\)
Cách giải:
Đặt \({z_1} = \frac{3}{2} + \frac{{\sqrt 7 }}{2}i;{z_2} = \frac{3}{2} - \frac{{\sqrt 7 }}{2}i\)\( \Rightarrow \left\{ \begin{array}{l}S = {z_1} + {z_2} = 3\\P = {z_1}.{z_2} = 4\end{array} \right..\)
Vậy \({z_1};\,\,{z_2}\) là nghiệm của phương trình \({z^2} - 3z + 4 = 0.\)
Chọn C.
Câu 15 (NB)
Phương pháp:
Áp dụng công thức tính nguyên hàm của hàm lượng giác: \(\int {\sin kxdx} = - \frac{1}{k}\cos kx + C\).
Cách giải:
\(\int {f\left( x \right)dx = \int {\sin 2xdx} } \)\( = - \frac{1}{2}\cos 2x + C\)
Chọn A.
Câu 16 (NB)
Phương pháp:
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTCP \(\overrightarrow u \left( {a;b;c} \right)\) là: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\).
Cách giải:
Phương trình đường thẳng đi qua điểm \(M\left( {2;0; - 1} \right)\) và có 1 VTCP \(\overrightarrow a = \left( {2; - 3;1} \right)\) là: \(\left\{ \begin{array}{l}x = 2 + 2t\\y = - 3t\\z = - 1 + t\end{array} \right..\)
Chọn A.
Câu 17 (NB)
Phương pháp:
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành, đường thẳng \(x = a;\) \(x = b\) quanh trục hoành bằng \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
Cách giải:
Thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^2} - 2x\), trục hoành, đường thẳng \(x = 0,\) \(x = 1\) quanh trục hoành là: \(V = \pi \int\limits_0^1 {{{\left( {{x^2} - 2x} \right)}^2}dx} = \frac{{8\pi }}{{15}}.\)
Chọn C.
Câu 18 (TH)
Phương pháp:
Sử dụng công thức tích phân Newton – Leibniz: \(\int\limits_a^b {f'\left( x \right)dx} = f\left( b \right) - f\left( a \right)\).
Cách giải:
\(\int\limits_{ - 1}^2 {f'\left( x \right)dx} = \left. {f\left( x \right)} \right|_{ - 1}^2\)\( = f\left( 2 \right) - f\left( { - 1} \right) = - 1 - 8 = - 9\)
Chọn A.
Câu 19 (TH)
Phương pháp:
- Bán kính của mặt cầu có tâm \(I\) và tiếp xúc với mặt phẳng \(\left( P \right)\) chính bằng khoảng cách từ \(I\) đến \(\left( P \right)\).
- Khoảng cách từ \(I\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là : \(d\left( {I;\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Cách giải:
Vì mặt cầu tâm I tiếp xúc với mặt phẳng \(\left( P \right)\) nên \(R = d\left( {I;\left( P \right)} \right).\)
Ta có \(d\left( {I;\left( P \right)} \right) = \frac{{\left| {1 + 2.2 - 2.\left( { - 3} \right) - 2} \right|}}{{\sqrt {{1^2} + {2^2} + {{\left( { - 2} \right)}^2}} }}\)\( = \frac{9}{3} = 3\)
Vậy bán kính mặt cầu cần tìm là \(R = 3\).
Chọn C.
Câu 20 (TH)
Phương pháp:
Mặt cầu \(\left( S \right):\)\({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) có tâm \(I\left( {a;b;c} \right)\) bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Cách giải:
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 8x + 2y + 1 = 0\) có tâm \(I\left( {4; - 1;0} \right)\) và bán kính \(R = \sqrt {{4^2} + {{\left( { - 1} \right)}^2} + {0^2} - 1} = 4.\)
Chọn A.
Câu 21 (TH)
Phương pháp:
- Tính khoảng cách từ I xuống : Khoảng cách từ \(I\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là : \(d\left( {I;\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
- Tính bán kính đường tròn giao tuyến \(r\), sử dụng công thức \(S = \pi {r^2}\).
- Áp dụng định lý Pytago để tính bán kính mặt cầu: \({R^2} = {r^2} + {d^2}\).
- Viết phương trình mặt cầu khi biết tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Cách giải:
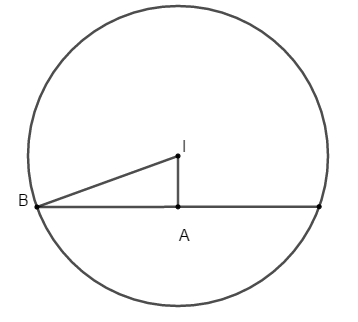
Ta có \(I\left( {1;2;0} \right);\) \(\left( P \right):2x - 2y + z - 7 = 0\)
\( \Rightarrow d\left( {I;\left( P \right)} \right) = \frac{{\left| {2.1 - 2.2 + 0 - 7} \right|}}{{\sqrt {4 + 4 + 1} }} = 3.\)
Đường tròn tâm A có \(S = 16\pi \)\( \Rightarrow \pi .A{B^2} = 16\pi \Rightarrow AB = 4\)
Áp dụng định lý Pyatgo trong tam giác ABI có \(I{B^2} = I{A^2} + A{B^2} = {3^2} + {4^2}\)\( \Rightarrow R = IB = 5\)
Mặt cầu tâm \(I\left( {1;2;0} \right)\) bán kính \(R = 5\) có phương trình là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 25.\)
Chọn C.
Câu 22 (TH)
Phương pháp:
Sử dụng phương pháp tích phân từng phần: \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \).
Cách giải:
Gọi \(I = \int\limits_0^1 {\left( {x - 2} \right){e^{2x}}dx} \)
Đặt \(\left\{ \begin{array}{l}u = x - 2\\dv = {e^{2x}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = \frac{{{e^{2x}}}}{2}\end{array} \right..\)
Khi đó ta có:
\(\begin{array}{l}I = \left. {\left( {x - 2} \right)\frac{{{e^{2x}}}}{2}} \right|_0^1 - \int\limits_0^1 {\frac{{{e^{2x}}}}{2}dx} \\\,\,\, = - \frac{1}{2}{e^2} + 1 - \left. {\frac{{{e^{2x}}}}{4}} \right|_0^1\\\,\,\, = - \frac{1}{2}{e^2} + 1 - \frac{{{e^2}}}{4} + \frac{1}{4}\\\,\,\, = - \frac{3}{4}{e^2} + \frac{5}{4} = \frac{{5 - 3{e^2}}}{4}\end{array}\)
Chọn A.
Câu 23 (TH)
Phương pháp:
Sử dụng phương pháp nguyên hàm từng phần: \(\int {udv} = uv - \int {vdu} + C\).
Cách giải:
Ta có \(\int {f\left( x \right)dx = \int {x\sin x} dx} \)
Đặt \(\left\{ \begin{array}{l}u = x\\dv = \sin xdx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = - \cos x\end{array} \right.\)
Khi đó \(\int {f\left( x \right) = - x\cos x + \int {\cos xdx} + C} \)\( = - x\cos x + \sin x + C\)
Chọn D.
Câu 24 (TH)
Phương pháp:
- Tìm hoành độ giao điểm của hai đồ thị hàm số.
- Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Cách giải:
Xét phương trình hoành độ giao điểm \(4x - {x^2} = 2x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\)
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số trên là:
\(S = \int\limits_0^2 {\left| {{x^2} - 2x} \right|dx} \)\( = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} = \frac{4}{3}.\)
Chọn D.
Câu 25 (TH)
Phương pháp:
Sử dụng phương pháp đổi biến số, đặt \(t = 2x - 3\).
Cách giải:
Đặt \(t = 2x - 3 \Rightarrow dt = 2xdx\).
Khi đó ta có: \(\int {f\left( {2x - 3} \right)dx} = \frac{1}{2}\int {f\left( t \right)dt} \).
Mà \(\int {f\left( x \right)dx} = F\left( x \right) + C\) nên \(\int {f\left( t \right)dt} = F\left( t \right) + C\)\( = F\left( {2x - 3} \right) + C\)
Vậy \(\int {f\left( {2x - 3} \right)dx} = \frac{1}{2}F\left( {2x - 3} \right) + C\).
Chọn B.
Câu 26 (TH)
Phương pháp:
Tìm nghiệm của phương trình rồi tìm tính.
Cách giải:
Ta có
\(\begin{array}{l}{z^2} - 2z + 5 = 0\\ \Leftrightarrow \left\{ \begin{array}{l}{z_1} = 1 + 2i\\{z_2} = 1 - 2i\end{array} \right.\\ \Rightarrow {\left| {{z_1}} \right|^2} = {\left| {{z_2}} \right|^2} = 5\\ \Rightarrow {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 10\end{array}\)
Chọn A.
Câu 27 (NB)
Phương pháp:
Mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\overrightarrow n \left( {A;B;C} \right)\) có phương trình \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Cách giải:
Mặt phẳng đi qua \(M\left( {2; - 3;4} \right)\) và có vecto pháp tuyến \(\overrightarrow n = \left( { - 2;4;1} \right)\) có phương trình là
\( - 2\left( {x - 2} \right) + 4\left( {y + 3} \right) + \left( {z - 4} \right) = 0\)\( \Leftrightarrow 2x - 4y - z - 12 = 0\)
Chọn A.
Câu 28 (TH)
Phương pháp:
Áp dụng \({i^2} = - 1\).
Cách giải:
Ta có \(z = 2019 + {i^{2019}} = 2019 + i.{\left( {{i^2}} \right)^{1009}}\)\( = 2019 + i\left( { - 1} \right) = 2019 - i\)
Vậy z có phần ảo bằng \( - 1.\)
Chọn B.
Câu 29 (NB)
Phương pháp:
Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).
Cách giải:
Ta có \(z = - 1 + i\)\( \Rightarrow \left| z \right| = \sqrt {{{\left( { - 1} \right)}^2} + {1^2}} = \sqrt 2 \)
Chọn D.
Câu 30 (NB)
Phương pháp:
Số phức \(z = a + bi\) có số phức liên hợp \(\overline z = a - bi\).
Cách giải:
Ta có \(\overline z = 2 - i \Rightarrow z = 2 + i.\)
Chọn A.
Câu 31 (VD)
Phương pháp:
- Đặt ẩn \(z = a + bi\), rút a theo b rồi tính.
- Tính \(\left| z \right| = \sqrt {{a^2} + {b^2}} \), thế \(a\) theo \(b\) và tìm GTNN bằng cách đưa biểu thức về dạng hằng đẳng thức.
Cách giải:
Đặt \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\)
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {iz - 3} \right| = \left| {z - 2 - i} \right|\\ \Leftrightarrow \left| {i\left( {a + bi} \right) - 3} \right| = \left| {a + bi - 2 - i} \right|\\ \Leftrightarrow \left| {\left( { - 3 - b} \right) + ai} \right| \\= \left| {\left( {a - 2} \right) + \left( {b - 1} \right)i} \right|\\ \Leftrightarrow {\left( {b + 3} \right)^2} + {a^2} \\= {\left( {a - 2} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow {b^2} + 6b + 9 + {a^2} \\= {a^2} - 4a + 4 + {b^2} - 2b + 1\\ \Leftrightarrow 4a + 8b + 4 = 0\\ \Leftrightarrow a + 2b + 1 = 0\\ \Leftrightarrow a = - 2b - 1\end{array}\)
Ta có:
\(\begin{array}{l}\left| z \right| = \sqrt {{a^2} + {b^2}} = \sqrt {{{\left( {2b + 1} \right)}^2} + {b^2}} \\\,\,\,\,\,\, = \sqrt {5{b^2} + 4b + 1} = \sqrt {5\left( {{b^2} + \frac{4}{5}b} \right) + 1} \\\,\,\,\,\,\, = \sqrt {5\left( {{b^2} + 2.b.\frac{2}{5} + \frac{4}{{25}}} \right) - \frac{4}{5} + 1} \\\,\,\,\,\,\, = \sqrt {5{{\left( {b + \frac{2}{5}} \right)}^2} + \frac{1}{5}} \ge \frac{{\sqrt 5 }}{5}\end{array}\)
Dấu bằng xảy ra khi và chỉ khi \(b = - \frac{2}{5} \Rightarrow a = - \frac{1}{5}.\)
Vậy \({\mathop{\rm Re}\nolimits} z = a = - \frac{1}{5}\).
Chọn D.
Câu 32 (VD)
Phương pháp:
- Sử dụng phương pháp nguyên hàm từng phần: \(\int {udv} = uv - \int {vdu} + C\).
- Đồng nhất hệ số tìm \(a,\,\,b,\,\,c\).
Cách giải:
Ta có \(F\left( x \right) = \int {f\left( x \right)} = \int {\left( {x - 2} \right)\sin 3x} \).
Đặt \(\left\{ \begin{array}{l}u = x - 2\\dv = \sin 3xdx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = - \frac{1}{3}\cos 3x\end{array} \right.\)
\(\begin{array}{l} \Rightarrow F\left( x \right) = \int {f\left( x \right)dx} \\ = - \frac{1}{3}\left( {x - 2} \right)\cos 3x + \frac{1}{3}\int {\cos 3xdx} \\ = - \frac{{\left( {x - 2} \right)\cos 3x}}{3} + \frac{1}{9}\sin 3x + C\end{array}\)
Mà \(F\left( x \right) = - \frac{{\left( {x - a} \right)\cos 3x}}{b} + \frac{1}{c}\sin 3x + 2019\)
Nên \(a = 2;\,\,b = 3;\,\,c = 9.\)
Vậy \(ab + c = 2.3 + 9 = 15.\)
Chọn C.
Câu 33 (VD)
Phương pháp:
- Tìm tích có hướng \(\left[ {\overrightarrow m ;\overrightarrow n } \right]\).
- Vì \(\overrightarrow p \) cùng hướng với \(\left[ {\overrightarrow m ;\overrightarrow n } \right]\) nên \(\overrightarrow p = k\left[ {\overrightarrow m ;\overrightarrow n } \right]\) với \(k > 0\).
- Tìm \(\overrightarrow p \) và tính \(\left| {\overrightarrow p } \right|\), từ đó tìm được hằng số \(k\).
Cách giải:
Ta có \(\overrightarrow m = \left( {4;3;1} \right);\,\,\overrightarrow n = \left( {0;0;1} \right)\)\( \Rightarrow \left[ {\overrightarrow m ;\overrightarrow n } \right] = \left( {3; - 4;0} \right).\)
Mà \(\overrightarrow p ;\left[ {\overrightarrow m ;\overrightarrow n } \right]\) cùng hường nên \(\overrightarrow p = \left( {3k; - 4k;0} \right);\left( {k > 0} \right)\)
Theo bài ra ta có: \(\left| {\overrightarrow p } \right| = 15\)
\(\begin{array}{l} \Rightarrow \sqrt {{{\left( {3k} \right)}^2} + {{\left( {4k} \right)}^2}} = 15\\ \Leftrightarrow \sqrt {25{k^2}} = 15\\ \Leftrightarrow 5k = 15\,\,\left( {Do\,\,k > 0} \right)\\ \Leftrightarrow k = 3\end{array}\)
Vậy \(\overrightarrow p = \left( {9; - 12;0} \right).\)
Chọn B.
Câu 34 (VD)
Phương pháp:
- Sử dụng tính chất hình thang cân: ABCD là hình thang cân nên \(\left\{ \begin{array}{l}AD = BC\\AB\parallel CD\end{array} \right.\)
- \(\overrightarrow {BA} ,\,\,\overrightarrow {CD} \) cùng hướng nên \(\overrightarrow {CD} = k\overrightarrow {BA} \,\,\left( {k > 0} \right)\), tham số hóa tọa độ điểm \(D\).
- Thay vào biểu thức \(AD = BC\) rồi tìm D.
- Loại trường hợp \(\overrightarrow {AD} ,\,\,\overrightarrow {BC} \) cùng phương.
Cách giải:
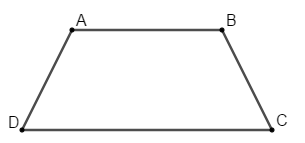
Vì \(ABCD\) là hình thang cân nên \(\left\{ \begin{array}{l}AD = BC\\AB\parallel CD\end{array} \right.\)
Ta có: \(A\left( {3;1; - 2} \right);\,\,\,B\left( { - 1;3;2} \right);\)\(C\left( { - 6;3;6} \right);\,\,\,D\left( {a;b;c} \right)\)
\( \Rightarrow \overrightarrow {BA} = \left( {4; - 2; - 4} \right);\)\(\overrightarrow {CD} = \left( {a + 6;b - 3;c - 6} \right)\)
Vì \(\overrightarrow {BA} ,\,\,\overrightarrow {CD} \) cùng hướng nên \(\overrightarrow {CD} = k\overrightarrow {BA} \,\,\left( {k > 0} \right)\), khi đó ta có:
\(\left\{ \begin{array}{l}a + 6 = 4k\\b - 3 = - 2k\\c - 6 = - 4k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4k - 6\\b = - 2k + 3\\c = - 4k + 6\end{array} \right.\) \( \Rightarrow D\left( {4k - 6; - 2k + 3; - 4k + 6} \right)\).
Vì \(ABCD\) là hình thang cân nên \(AD = BC \Leftrightarrow A{D^2} = B{C^2}\).
\(\begin{array}{l} \Leftrightarrow {\left( {4k - 9} \right)^2} + {\left( { - 2k + 2} \right)^2} + {\left( { - 4k + 8} \right)^2}\\ = {\left( { - 5} \right)^2} + {0^2} + {4^2}\\ \Leftrightarrow 36{k^2} - 144k + 108 = 0\\ \Leftrightarrow \left[ \begin{array}{l}k = 3\\k = 1\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)
Với \(k = 3 \Rightarrow D\left( {6; - 3; - 6} \right)\).
Khi đó ta có: \(\overrightarrow {AD} = \left( {3; - 4; - 4} \right),\,\,\overrightarrow {BC} = \left( { - 5;0;4} \right)\) không cùng phương (thỏa mãn).
Với \(k = 1 \Rightarrow D\left( { - 2;1;2} \right)\).
Khi đó ta có: \(\overrightarrow {AD} = \left( { - 5;0;4} \right),\,\,\overrightarrow {BC} = \left( { - 5;0;4} \right)\) cùng phương (không thỏa mãn).
Vậy \(D\left( {6; - 3; - 6} \right) \Rightarrow a + b + c = - 3.\)
Chọn D.
Câu 35 (VDC)
Phương pháp:
- Lập BBT của hàm số \(y = f\left( x \right)\).
- So sánh \(f\left( 0 \right)\) với \(f\left( { - 1} \right),\,\,f\left( 2 \right)\).
- Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = - 1,\,\,x = 0\) và trục hoành, \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = 0,\,\,x = 2\) và trục hoành.
- Giải bất phương trình \({S_2} > {S_1}\).
Cách giải:
Dựa vào đồ thị hàm số ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 2\end{array} \right.\)
Bảng biến thiên:
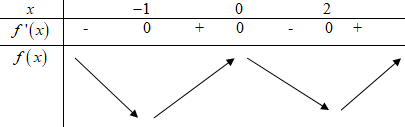
Dựa vào bảng biến thiên ta thấy \(f\left( 0 \right) > f\left( { - 1} \right).\,\,f\left( 0 \right) > f\left( 2 \right)\).
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = - 1,\,\,x = 0\) và trục hoành, ta có: \({S_1} = \int\limits_{ - 1}^0 {\left| {f'\left( x \right)dx} \right|} = \int\limits_{ - 1}^0 {f'\left( x \right)dx} \)\( = f\left( 0 \right) - f\left( { - 1} \right) > 0\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f'\left( x \right)\), đường thẳng \(x = 0,\,\,x = 2\) và trục hoành, ta có:
\(\begin{array}{l}{S_2} = \int\limits_0^2 {\left| {f'\left( x \right)dx} \right|} \\ = - \int\limits_0^2 {f'\left( x \right)dx} \\ = - \left[ {f\left( 2 \right) - f\left( 0 \right)} \right]\\ = f\left( 0 \right) - f\left( 2 \right) > 0\end{array}\).
Dựa vào đồ thị hàm số ta thấy được:
\(\begin{array}{l}{S_2} > {S_1}\\ \Leftrightarrow f\left( 0 \right) - f\left( 2 \right) > f\left( 0 \right) - f\left( { - 1} \right)\\ \Leftrightarrow f\left( 2 \right) < f\left( { - 1} \right)\end{array}\).
Vậy \(f\left( 0 \right) > f\left( { - 1} \right) > f\left( 2 \right)\).
Chọn B.
Câu 36 (VD)
Phương pháp:
- Tìm tọa độ điểm \(M\) biểu diễn số phức \(z\).
- Tìm hàm số biểu thị mối liên hệ giữa tọa độ diểm \(M\) không phụ thuộc vào \(m\).
- Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Cách giải:
Ta có điểm biểu diễn của số phức z là \(M\left( {m - 2;{m^2} - 1} \right) \Rightarrow \left\{ \begin{array}{l}x = m - 2\\y = {m^2} - 1\end{array} \right.\)
\( \Rightarrow y + 1 = {\left( {x + 2} \right)^2}\)\( \Leftrightarrow y = {x^2} + 4x + 3\)
\( \Rightarrow \left( C \right):\,\,y = {x^2} + 4x + 3\) là 1 parabol.
Hoành độ giao điểm của đồ thị hàm số \(y = {x^2} + 4x + 3\) với trục hoành là: \({x^2} + 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\end{array} \right.\)
Diện tích hình phẳng cần tìm là \(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} + 4x + 3} \right|dx} \)\( = - \int\limits_{ - 3}^{ - 1} {\left( {{x^2} + 4x + 3} \right)} = \frac{4}{3}.\)
Chọn A.
Câu 37 (VD)
Phương pháp:
- \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \frac{1}{4}{x^2}\), trục hoành, đường thẳng \(x = 0\) và \(x = 4\).
- Cho hai hàm số \(f\left( x \right);g\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\). Diện tích hình phẳng giới hạn bởi đồ thị \(y = f\left( x \right),y = g\left( x \right)\) và các đường thẳng \(x = a,x = b\) bằng \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
- Tính \({S_1} = {S_{OABC}} - {S_2}\).
- Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}\).
Cách giải:
Ta thấy \({S_2}\) là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \frac{1}{4}{x^2}\), trục hoành, đường thẳng \(x = 0\) và \(x = 4\) nên \({S_2} = \int\limits_0^4 {\frac{1}{4}{x^2}dx} = \frac{{16}}{3}.\)
Ta có: \(OABC\) là hình vuông cạnh \(4\) nên \({S_{ABCO}} = {4^2} = 16\).
\( \Rightarrow {S_1} = {S_{OABC}} - {S_2} = 16 - \frac{{16}}{3} = \frac{{32}}{3}.\)
Vậy \(\frac{{{S_1}}}{{{S_2}}} = \frac{{32}}{3}:\frac{{16}}{3} = 2.\)
Chọn D.
Câu 38 (VD) – Tích phân
Phương pháp:
- Biến đổi lượng giác: \(\frac{1}{{1 + \sin x}} = \frac{{1 - \sin x}}{{1 - {{\sin }^2}x}}\)\( = \frac{{1 - \sin x}}{{{{\cos }^2}x}} = \frac{1}{{{{\cos }^2}x}} - \frac{{\sin x}}{{{{\cos }^2}x}}\)
- Tách thành 2 tích phân, sử dụng công thức nguyên hàm cơ bản \(\int {\frac{1}{{{{\cos }^2}x}}dx} = \tan x + C\) và phương pháp đổi biến.
- Đồng nhất hệ số tìm \(a,\,\,b,\,\,c\) và tính tổng \(a + b + c\).
Cách giải:
Ta có \(\frac{1}{{1 + \sin x}} = \frac{{1 - \sin x}}{{1 - {{\sin }^2}x}}\)\( = \frac{{1 - \sin x}}{{{{\cos }^2}x}} = \frac{1}{{{{\cos }^2}x}} - \frac{{\sin x}}{{{{\cos }^2}x}}\)
Khi đó:
\(\begin{array}{l}I = \int\limits_0^{\frac{\pi }{6}} {\frac{{dx}}{{1 + \sin x}}} \\ = \int\limits_0^{\frac{\pi }{6}} {\left( {\frac{1}{{{{\cos }^2}x}} - \frac{{\sin x}}{{{{\cos }^2}x}}} \right)dx} \\ \Leftrightarrow I = \left. {\tan x} \right|_0^{\frac{\pi }{6}} - \int\limits_0^{\frac{\pi }{6}} {\frac{{\sin x}}{{{{\cos }^2}x}}dx} \\ \Leftrightarrow I = \frac{{\sqrt 3 }}{3} - {I_1}\end{array}\)
Đặt \(t = \cos x \Rightarrow dt = - \sin xdx\).
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = \frac{\pi }{6} \Rightarrow t = \frac{{\sqrt 3 }}{2}\end{array} \right.\).
Khi đó \({I_1} = - \int\limits_1^{\frac{{\sqrt 3 }}{2}} {\frac{{dt}}{{{t^2}}}} = \left. {\frac{1}{t}} \right|_1^{\frac{{\sqrt 3 }}{2}}\)\( = \frac{2}{{\sqrt 3 }} - 1 = \frac{{2\sqrt 3 - 3}}{3}\)
Vậy \(I = \frac{{\sqrt 3 }}{3} - \frac{{2\sqrt 3 - 3}}{3}\) \( = \frac{{\sqrt 3 - 2\sqrt 3 + 3}}{3} = \frac{{ - \sqrt 3 + 3}}{3}\)
Mà \(I = \frac{{a\sqrt 3 + b}}{c}\)\( \Rightarrow a = - 1;\,\,b = 3;\,\,c = 3.\)
Vậy \(a + b + c\) \( = - 1 + 3 + 3 = 5.\)
Chọn D.
Câu 39 (VD)
Phương pháp:
- Tìm bán kính của mặt cầu: Mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} - 2ax - 2by - 2cz + d = 0\) có bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
- Tính khoảng cách từ tâm I của mặt cầu đến đường thẳng \(\left( \Delta \right)\) dựa vào định lí Pytago.
- Sử dụng công thức tính khoảng cách từ \(I\) đến \(\Delta \) là: \(d\left( {I;\left( \Delta \right)} \right) = \frac{{\left| {\left[ {\overrightarrow {IM} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}}\) với \(\overrightarrow u \) là 1 VTCP của đường thẳng \(\Delta \), \(M\) là điểm bất kì trên đường thẳng \(\Delta \).
- Giải phương trình tìm \(m\).
Cách giải:

Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 4x - 6y + m = 0\) có tâm \(I\left( { - 2;3;0} \right)\) và bán kính \(R = \sqrt {4 + 9 - m} = \sqrt {13 - m} \) với \(m \le 13\).
Gọi \(O\) là trung điểm của \(AB \Rightarrow IO \bot AB\) và \(OA = OB = \frac{1}{2}AB = 4\).
Đường thẳng \(\left( \Delta \right)\) có 1 vecto chỉ phương \(\overrightarrow u = \left( {2;1;2} \right)\) và \(M\left( {4;3;3} \right) \in \left( \Delta \right)\) bất kì.
Ta có: \(\overrightarrow {IM} = \left( {6;0;3} \right)\)\( \Rightarrow \left[ {\overrightarrow {IM} ;\overrightarrow u } \right] = \left( { - 3; - 6;6} \right).\)
\( \Rightarrow d\left( {I;\left( \Delta \right)} \right) = \frac{{\left| {\left[ {\overrightarrow {IM} ;\overrightarrow n } \right]} \right|}}{{\left| {\overrightarrow n } \right|}}\)\( = \frac{{\sqrt {9 + 36 + 36} }}{{\sqrt {4 + 1 + 4} }} = 3 = IO\)
Áp dụng định lí Pytago trong tam giác vuông \(OAI\) ta có:
\(\begin{array}{l}I{A^2} = I{O^2} + O{A^2}\\ \Leftrightarrow 13 - m = 9 + 16\\ \Leftrightarrow m = - 12\,\,\left( {tm} \right)\end{array}\)
Chọn B.
Câu 40 (TH)
Phương pháp:
Áp dụng công thức \(s = \int {v\left( t \right)dt} \).
Cách giải:
Quãng đường mà ô tô đi được trong 15 giây cuối cùng là:
\(s = \int\limits_0^{15} {\left( { - 2t + 20} \right)dt} \)\( = \left. {\left( { - {t^2} + 20t} \right)} \right|_0^{15} = 75.\)
Chọn B.
Câu 41 (TH)
Phương pháp:
- \(\left\{ \begin{array}{l}AB \subset \left( Q \right)\\\left( Q \right) \bot \left( P \right)\end{array} \right. \Rightarrow \overrightarrow {{n_Q}} = \left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right]\) với \(\overrightarrow {{n_P}} ,\,\,\overrightarrow {{n_Q}} \) lần lượt là 1 VTPT của \(\left( P \right),\,\,\left( Q \right)\).
- Mặt phẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT là \(\overrightarrow n \left( {A;B;C} \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Cách giải:
Mặt phẳng \(\left( P \right)\) có 1 VTPT là \(\overrightarrow {{n_P}} = \left( {2; - 1;2} \right)\).
Ta có: \(A\left( {1;0; - 2} \right);B\left( { - 1; - 1;3} \right)\)\( \Rightarrow \overrightarrow {AB} = \left( { - 2; - 1;5} \right).\)
\( \Rightarrow \left[ {\overrightarrow {{n_P}} ;\overrightarrow {AB} } \right] = \left( { - 3; - 14; - 4} \right).\).
Gọi \(\overrightarrow {{n_Q}} \) là 1 VTPT của mặt phẳng \(\left( Q \right)\) ta có: \(\left\{ \begin{array}{l}AB \subset \left( Q \right)\\\left( Q \right) \bot \left( P \right)\end{array} \right. \)
\(\Rightarrow \overrightarrow {{n_Q}} = \left[ {\overrightarrow {AB} ;\overrightarrow {{n_P}} } \right] = \left( { - 3; - 14; - 4} \right)\) là 1 VTPT của mặt phẳng \(\left( Q \right)\).
Vậy phương trình mặt phẳng \(\left( Q \right)\) là:
\( - 3\left( {x - 1} \right) - 14\left( {y - 0} \right) - 4\left( {z + 2} \right) = 0\) \( \Leftrightarrow 3x + 14y + 4z + 5 = 0\)
Chọn D.
Câu 42 (VD)
Phương pháp:
Sử dụng phương pháp tích phân từng phần: \(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu} \).
Cách giải:
Gọi \(I = \int\limits_0^4 {xf'\left( {\frac{x}{2}} \right)dx} \)
Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( {\frac{x}{2}} \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = 2f\left( {\frac{x}{2}} \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow I = \left. {2xf\left( {\frac{x}{2}} \right)} \right|_0^4 - 2\int\limits_0^4 {f\left( {\frac{x}{2}} \right)dx} \\ \Leftrightarrow I = 8f\left( 2 \right) - 4\int\limits_0^4 {f\left( {\frac{x}{2}} \right)d\left( {\frac{x}{2}} \right)} \\ \Leftrightarrow I = 8.16 - 4\int\limits_0^8 {f\left( x \right)dx} \\ \Leftrightarrow I = 128 - 4.4 = 112.\end{array}\)
Chọn A.
Câu 43 (VD)
Phương pháp:
- Đổi biến \(t = {x^2} + 2\).
- Đồng nhất hệ số tìm \(a,\,\,b\).
Cách giải:
Đặt \({x^2} + 2 = t \Rightarrow 2xdx = dt\)
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 2\\x = 1 \Rightarrow t = 3\end{array} \right.\).
Khi đó ta có:
\(\begin{array}{l}I = \int\limits_0^1 {x{e^{{x^2} + 2}}dx} = \frac{1}{2}\int\limits_2^3 {{e^t}dt} \\I = \left. {\frac{1}{2}{e^t}} \right|_2^3 = \frac{1}{2}\left( {{e^3} - {e^2}} \right)\end{array}\)
Mà \(I = \frac{a}{2}\left( {{e^b} - {e^c}} \right)\)\( \Rightarrow a = 1;\,\,\,b = 3;\,\,c = 2\)
Vậy \(a + b + c = 1 + 3 + 2 = 6.\)
Chọn D.
Câu 44 (VD)
Phương pháp:
- Số phức là một số thực khi nó có phần ảo bằng 0. Từ đó tìm \(m\) và suy ra số phức \(z\).
- Thay số phức \(z\) tìm được tính giá trị biểu thức đề bài yêu cầu.
Cách giải:
Vì \(z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\) là số thực nên \(m - 2 = 0 \Leftrightarrow m = 2.\)
Suy ra \(z = {m^2} - 3m + 3 = 1.\)
Vậy \(1 + z + {z^2} + ... + {z^{2019}}\)\( = 1 + 1 + 1 + ... + 1 = 2020\) (có 2020 số 1).
Chon D.
Câu 45 (TH)
Phương pháp:
Hai đường thẳng \({d_1},\,\,{d_2}\) cắt nhau khi và chỉ khi \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {AM} = 0\) với \(\overrightarrow {{u_1}} ,\,\,\overrightarrow {{u_2}} \) lần lượt là 1 VTCP của đường thẳng \({d_1},\,\,{d_2}\), \(M\) là điểm bất kì thuộc đường thẳng \({d_1}\).
Cách giải:
Đường thẳng \({d_1}\) có 1 VTCP là \(\overrightarrow {{u_1}} = \left( {1; - 2;1} \right)\) và đi qua điểm \(M\left( {1;2;3} \right)\).
Ta có: \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow u } \right] = \left( { - 5;a - 2;1 + 2a} \right)\) và \(\overrightarrow {AM} = \left( {0;2;4} \right)\).
Để \({d_1},\,\,{d_2}\) cắt nhau thì \(\left[ {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right].\overrightarrow {AM} = 0\).
\(\begin{array}{l} \Leftrightarrow - 5.0 + \left( {a - 2} \right).2 + \left( {1 - 2a} \right).4 = 0\\ \Leftrightarrow 2a - 4 + 4 - 8a = 0\\ \Leftrightarrow a = 0.\end{array}\)
Chọn C.
Câu 46 (VD)
Phương pháp:
- Tìm điểm \(I\) sao cho \(\overrightarrow {IA} + \overrightarrow {IB} = 0\)
- Phân tích và chứng minh \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
- Khi đó \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|\) nhỏ nhất thì \(MI\) nhỏ nhất \( \Leftrightarrow M\) là hình chiếu của \(I\) trên \(\left( {Oxy} \right)\).
Cách giải:
Ta tìm điểm I sao cho \(\overrightarrow {IA} + \overrightarrow {IB} = 0\)\( \Rightarrow I\) là trung điểm của \(AB\).
Ta có \(A\left( {3;5; - 1} \right);B\left( {1;1;3} \right) \Rightarrow I\left( {2;3;1} \right).\)
Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {IB} = 2\overrightarrow {MI} \) \( \Rightarrow \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {2\overrightarrow {MI} } \right| = 2MI\).
Khi đó \({\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|_{\min }} \Leftrightarrow M{I_{\min }} \Leftrightarrow M\) là hình chiếu của \(I\) trên \(\left( {Oxy} \right)\).
Mà \(I\left( {2;3;1} \right) \Rightarrow M\left( {2;3;0} \right)\).
Chọn B.
Câu 47 (VD)
Phương pháp:
- Mặt cầu \(\left( S \right)\) tâm O và tiếp xúc với mặt phẳng \(\left( P \right):x - 2y + 2z + 9 = 0\) tại điểm \(H\left( {a;b;c} \right)\) nên \(H\) là hình chiếu của \(O\) lên \(\left( P \right)\).
- Viết phương trình đường thẳng \(OH\) đi qua \(O\) và vuông góc với \(\left( P \right)\).
- Tìm \(H = OH \cap \left( P \right)\).
- Xác định \(a,\,\,b,\,\,c\) và tính tổng.
Cách giải:
Vì mặt cầu \(\left( S \right)\) tâm O và tiếp xúc với mặt phẳng \(\left( P \right):x - 2y + 2z + 9 = 0\) tại điểm \(H\left( {a;b;c} \right)\) nên \(H\) là hình chiếu của \(O\) lên \(\left( P \right)\).
\( \Rightarrow OH \bot \left( P \right)\)\( \Rightarrow \overrightarrow {{u_{OH}}} = \overrightarrow {{n_P}} = \left( {1; - 2;2} \right)\).
Phương trình đường thẳng \(OH\) là: \(\left\{ \begin{array}{l}x = t\\y = - 2t\\z = 2t\end{array} \right.\).
Vì \(H \in OH \Rightarrow H\left( {t; - 2t;2t} \right)\).
Lại có \(H \in \left( P \right) \Rightarrow t - 2.\left( { - 2t} \right) + 2.2t + 9 = 0\) \( \Leftrightarrow 9t + 9 = 0 \Leftrightarrow t = - 1\).
\( \Rightarrow H\left( { - 1;2; - 2} \right)\).
\( \Rightarrow a = - 1,\,\,b = 2,\,\,c = - 2\)
Vậy \(a + b + c = - 1 + 2 + \left( { - 2} \right) = - 1.\)
Chọn B.
Câu 48 (VD)
Phương pháp:
- Gọi \(H = d \cap \left( P \right)\), khi đó \(H = d \cap d'\). Xác định tọa độ điểm \(H\).
- \(\left\{ \begin{array}{l}d' \subset \left( P \right)\\d \bot d'\end{array} \right. \Rightarrow \overrightarrow {{u_{d'}}} = \left[ {\overrightarrow {{u_d}} ;\overrightarrow {{n_P}} } \right]\).
- Viết phương trình đường thẳng đi qua \(H\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTCP \(\overrightarrow u \left( {a;b;c} \right)\) là \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\).
Cách giải:
Gọi \(H = d \cap \left( P \right)\).
Vì \(H \in d \Rightarrow H\left( {2t;3 + t;2 - 3t} \right).\)
Mà \(H \in \left( P \right)\)\( \Rightarrow 2t - \left( {3 + t} \right) + 2\left( {2 - 3t} \right) - 6 = 0\)
\( \Leftrightarrow - 5t - 5 = 0 \Leftrightarrow t = - 1\)
\( \Rightarrow H\left( { - 2;2;5} \right)\)
Gọi đường thẳng cần tìm là \(d'\). Vì \(d' \subset \left( P \right)\) và \(d'\) cắt \(d\) nên \(H \in d'\) .
Gọi \(\overrightarrow {{u_d}} = \left( {2;1; - 3} \right)\) là 1 VTCP của \(d\), \(\overrightarrow n \left( {1; - 1;2} \right)\) là 1 VTPT của \(\left( P \right)\).
Ta lại có: \(\left\{ \begin{array}{l}d' \subset \left( P \right)\\d \bot d'\end{array} \right.\)\( \Rightarrow \overrightarrow {{u_{d'}}} = \left[ {\overrightarrow {{u_d}} ;\overrightarrow {{n_P}} } \right] = \left( { - 1; - 7; - 3} \right)\) là 1 VTCP của đường thẳng \(d'\).
\( \Rightarrow \left( {1;7;3} \right)\) cũng là 1 VTCP của đường thẳng \(d'\).
Vậy phương trình đường thẳng \(d'\) cần tìm là: \(\frac{{x + 2}}{1} = \frac{{y - 2}}{7} = \frac{{z - 5}}{3}\).
Chọn A.
Câu 49 (TH)
Phương pháp:
- Áp dụng công thức tính nguyên hàm cơ bản: \(\int {{x^n}dx} = \frac{{{x^{n + 1}}}}{{n + 1}} + C\,\,\left( {n \ne - 1} \right)\) để tìm \(F\left( x \right).\)
- Sử dụng giả thiết \(F\left( 1 \right) = 1\) để tìm hằng số \(C\).
- Suy ra hàm số \(F\left( x \right)\) hoàn chỉnh và tính \(F\left( { - 1} \right)\).
Cách giải:
Ta có \(F\left( x \right) = \int {f\left( x \right) = \int {\left( {{x^2} + x} \right)dx} } \)\( \Rightarrow F\left( x \right) = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} + C\)
Mà \(F\left( 1 \right) = 1 \Leftrightarrow \frac{1}{3} + \frac{1}{2} + C = 1\)\( \Leftrightarrow C = \frac{1}{6}.\)
\( \Rightarrow F\left( x \right) = \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} + \frac{1}{6}.\)
Vậy \(F\left( { - 1} \right) = - \frac{1}{3} + \frac{1}{2} + \frac{1}{6} = \frac{1}{3}.\)
Chọn A.
Câu 50 (VD)
Phương pháp:
- Đặt \(z = a + bi \Rightarrow \overline z = a - bi\).
- Thay vào biểu thức, nhân chéo sau đó tìm \(a,\,\,b\).
- Suy ra số phức \(z\) và tính \({\rm{w}} = 1 + z + {z^2}\).
Cách giải:
Đặt \(z = a + bi \Rightarrow \overline z = a - bi\).
Theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\,\frac{{5\left( {\overline z + i} \right)}}{{z + 1}} = 2 - i\\ \Rightarrow \frac{{5\left( {a - bi + i} \right)}}{{a + bi + 1}} = 2 - i\\ \Leftrightarrow 5\left[ {a - \left( {b - 1} \right)i} \right] \\= \left( {a + 1 + bi} \right)\left( {2 - i} \right)\\ \Leftrightarrow 5a - 5\left( {b - 1} \right)i\\= 2\left( {a + 1} \right) + b + \left( {2b - a - 1} \right)i\\ \Leftrightarrow \left\{ \begin{array}{l}5a = 2a + 2 + b\\5 - 5b = 2b - a - 1\end{array} \right. \\\Rightarrow a = b = 1\\ \Rightarrow z = 1 + i \Rightarrow {z^2} = 2i\\ \Rightarrow {\rm{w}} = 1 + z + {z^2} = 1 + 1 + i + 2i \\= 2 + 3i\end{array}\)
Vậy \(\left| {\rm{w}} \right| = \sqrt {{2^2} + {3^2}} = \sqrt {13} .\)
Chọn C.
Nguồn: Sưu tầm
Loigiaihay.com
- Đề số 8 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12
- Đề số 9 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12
- Đề số 10 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12
- Đề số 6 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12
- Đề số 5 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 12
>> Xem thêm












Danh sách bình luận