Bài 50 trang 13 SBT Hình Học 11 Nâng cao

Giải bài 50 trang 13 sách bài tập Hình Học 11 Nâng cao. Chứng minh rằng hai tam giác vuông bằng nhau nếu có các cạnh huyền bằng nhau và đường cao ứng với cạnh huyền bằng nhau.

Đề bài

Chứng minh rằng hai tam giác vuông bằng nhau nếu có các cạnh huyền bằng nhau và đường cao ứng với cạnh huyền bằng nhau.

Lời giải chi tiết

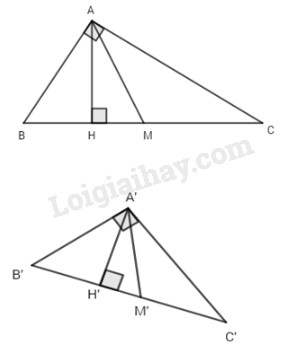
Cho hai tam giác ABC, A^’B^’C^’ vuông tại các đỉnh A, A^’. Có BC = B^’C^’ và hai đường cao AH, A^’H^’ bằng nhau.

Gọi AM, A^’M^’ là các đường trung tuyến thì AM = A^’M^’ và do đó hai tam giác vuông AHM và A^’H^’M^’ bằng nhau.

Gọi F là phép dời hình biến tam giác AHM thành tam giác A^’H^’M^’ thì dễ thấy rằng F biến đoạn thẳng BC thành đoạn thẳng B^’C^’ (hoặc thành đoạn thẳng C^’B^’).

Vậy hai tam giác đã cho bằng nhau.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 51 trang 13 SBT Hình Học 11 Nâng cao
Giải bài 51 trang 13 sách bài tập Hình Học 11 Nâng cao. Chứng minh rằng nếu ba trung tuyến của tam giác ABC lần lượt bằng ba trung tuyến của tam giác A’B’C’ thì hai tam giác đó bằng nhau.
Bài 52 trang 13 SBT Hình Học 11 Nâng cao
Giải bài 52 trang 13 sách bài tập Hình Học 11 Nâng cao. Chứng minh rằng nếu tam giác ABC bằng tam giác A’B’C’ thì hình H bằng hình H’.
Bài 49 trang 12 SBT Hình Học 11 Nâng cao
Giải bài 49 trang 12 sách bài tập Hình Học 11 Nâng cao. Chứng minh rằng hai tam giác bằng nhau nếu có các đường tròn nội tiếp bằng nhau, một cặp đường tròn bàng tiếp bằng nhau, đồng thời khoảng cách giữa tâm đường tròn nội tiếp và bàng tiếp của hai tam giác đó cũng bằng nhau.
Bài 48 trang 12 SBT Hình Học 11 Nâng cao
Giải bài 48 trang 12 sách bài tập Hình Học 11 Nâng cao. Chứng minh rằng hai hình thang ấy bằng nhau nếu AB = A’B’, BC = B’C’ và CD = C’D’.
Bài 47 trang 12 SBT Hình Học 11 Nâng cao
Giải bài 47 trang 12 sách bài tập Hình Học 11 Nâng cao . Cho hai tam giác ABC và A’B’C’ với đường cao lần lượt là AH và A’H’. Trong mỗi trường hợp dưới đây, hai tam giác đó có bằng nhau hay không?