-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Bài 3. Khái niệm về thể tích của khối đa diện
Giải bài 3 trang 25 SGK Hình học 12
Cho hình hộp ABCD.A’B’C’D’. Tính thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Đề bài
Cho hình hộp \(ABCD.A’B’C’D’\). Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện \(ACB’D’\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Gọi \(S\) là diện tích đáy \(ABCD\) và \(h\) là chiều cao của khối hộp. Tính thể tích của khối hộp.
+) Chia khối hộp thành khối tứ diện \(ACB’D’\) và bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\). Tính thể tích của bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\).
+) Suy ra \({V_{ACB'D'}} = V - \)\(\left( {{V_{A.A'B'D'}} + {V_{C.C'B'D'}} + {V_{B'BAC}} + {V_{D'.DAC}}} \right)\)
+) Tính tỉ số thể tích.
Lời giải chi tiết
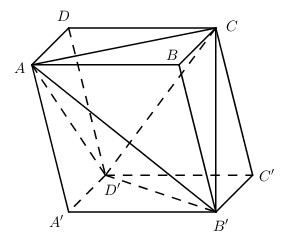
Gọi \(S\) là diện tích đáy \(ABCD\) và \(h\) là chiều cao của khối hộp thì thể tích của khối hộp: \( \Rightarrow V = S.h\)
Chia khối hộp thành khối tứ diện \(ACB’D’\) và bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\).
Xét khối chóp \(A.A'B'D'\) có diện tích đáy \({S_{A'B'D'}} = \dfrac{S}{2}\) và chiều cao bằng \(h\). Do đó \({V_{A.A'B'D'}} = \dfrac{1}{3}.\dfrac{S}{2}.h = \dfrac{{S.h}}{6}\).
Tương tự như vậy ta chứng minh được:
\({V_{A.A'B'D'}} = {V_{C.C'B'D'}} = {V_{B'BAC}} = {V_{D'.DAC}} \)\(= \dfrac{{S.h}}{6}\)
Vậy \({V_{ACB'D'}} = V - \)\(\left( {{V_{A.A'B'D'}} + {V_{C.C'B'D'}} + {V_{B'BAC}} + {V_{D'.DAC}}} \right)\)
\(= S.h - 4.\dfrac{{S.h}}{6} = \dfrac{{S.h}}{3}\).
\( \Rightarrow \dfrac{V}{{{V_{ACB'D'}}}} = \dfrac{{S.h}}{{\dfrac{1}{3}S.h}} = 3\)
Loigiaihay.com
Bình luận
Chia sẻ
- Giải bài 4 trang 25 SGK Hình học 12
- Giải bài 5 trang 26 SGK Hình học lớp 12
- Giải bài 6 trang 26 SGK Hình học lớp 12
- Giải bài 2 trang 25 SGK Hình học 12
- Giải bài 1 trang 25 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
