Phần câu hỏi bài 11 trang 129, 130 Vở bài tập toán 8 tập 1
Giải phần câu hỏi bài 11 trang 129, 130 VBT toán 8 tập 1. Cạnh của một hình thoi bằng 25, một đường chéo bằng 14 đường chéo kia bằng...
Câu 28.
Cạnh của một hình thoi bằng \(25\), một đường chéo bằng \(14\) đường chéo kia bằng
(A) \(48\) (B) \(24\)
(C) \(\sqrt {429} \) (D) \(28\)
Phương pháp giải:
Phương pháp giải:
Sử dụng:
- Hai đường chéo hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết:
Lời giải:
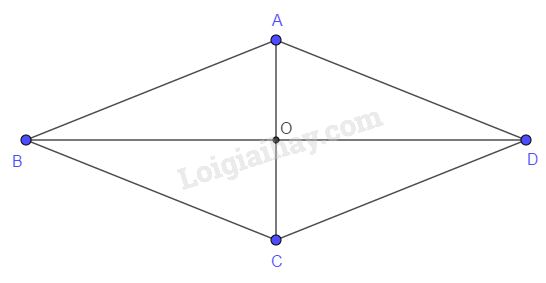
Xét hình thoi \(ABCD\), \(O\) là giao điểm hai đường chéo.
\(AB=25, AC=14\)
Theo tính chất hình thoi ta có \(OA=OC=AC:2=14:2=7\)
Áp dụng định lí Pytago vào tam giác vuông \(OAB\) vuông tại \(O\) ta có:
\(\eqalign{
& A{B^2} = O{A^2} + O{B^2} \cr
& \Rightarrow O{B^2} = A{B^2} - O{A^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {25^2} - {7^2} = 576 = {24^2} \cr
& \Rightarrow OB = 24 \cr
& \Rightarrow BD = 2OB = 2.24 = 48 \cr} \)
Chọn A.
Câu 29.
Hình thoi \(ABCD\) có cạnh bằng \(4\). Tổng \(A{C^2} + B{D^2}\) bằng
(A) \(64\) (B) \(32\)
(C) \(16\) (D) \(48\).
Phương pháp giải:
Phương pháp giải:
- Hai đường chéo hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết:
Phương pháp giải:
- Hai đường chéo hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Câu 30.
Đúng ghi Đ, sai ghi S vào ô trống:
(A) Hình bình hành \(ABCD\) là hình thoi nếu \(AB=CD\)
(B) Hình bình hành \(ABCD\) là hình thoi nếu \(BC=CD.\)
(C) Hình bình hành \(ABCD\) là hình thoi nếu \(AC\bot BD\).
(D) Hình bình hành \(ABCD\) là hình thoi nếu \(AC\) là đường phân giác của góc \(A\).
Phương pháp giải:
Dấu hiệu nhận biết
a) Tứ giác có bốn cạnh bằng nhau là hình thoi.
b) Hình bình hành có hai cạnh kề bằng nhau là hình thoi
c) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
d) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Lời giải chi tiết:
(A) S
\(AB=CD\) thì hình bình hành vẫn chỉ là hình bình hành chưa chắc là hình thoi.
(B) Đ (theo dấu hiệu nhận biết hình bình hành có hai cạnh kề bằng nhau là hình thoi)
(C) Đ (theo dấu hiệu nhận biết hình bình hành có hai đường chéo vuông góc với nhau là hình thoi)
(D) Đ (theo dấu hiệu nhận biết hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi).
Loigiaihay.com













Danh sách bình luận