Đề kiểm tra 45 phút chương 1 phần Đại số 8 - Đề số 2

Đề bài

Câu 1: Thực hiện phép tính

\(a)\,\,2{x^2}\left( {x - 2} \right) + 3x\left( {{x^2} - x - 2} \right) \)\(- 5\left( {3 - {x^2}} \right)\)

\(b)\,\,\left( {x - 1} \right)\left( {x - 3} \right) - \left( {4 - x} \right)\left( {2x + 1} \right) \)\(- 3{x^2} + 2x - 5\)

Câu 2: Rút gọn biểu thức

\(a)\,\,\left( {x - y} \right)\left( {x + y} \right)\left( {{x^2} + {y^2}} \right)\)\(.\left( {{x^4} + {y^4}} \right)\)

\(b)\,\,\left( {x + 2} \right)\left( {{x^2} + 2x + 4} \right) - {\left( {x - 2} \right)^3} \)\(- 6\left( {x - 1} \right)\left( {x + 1} \right)\)

Câu 3: Phân tích các đa thức sau thành nhân tử

\(\begin{array}{l}a)\,\,3{x^3} - 3{x^2}y - 6{x^2} + 6xy\\b)\,\,4{x^2} - 20xy + 25 - {\left( {3x - 2} \right)^2}\\c)\,\,{x^2} - 6x + 5 + {\left( {x - 5} \right)^2}\end{array}\)

Câu 4: Thực hiện phép chia

\(\begin{array}{l}a)\,\,\left( {6{x^2} - 11x - 10} \right):\left( {3x + 2} \right)\\b)\,\,\left( {{x^4} + 2{x^3} + 10x - 25} \right):\left( {{x^2} + 5} \right)\end{array}\)

Lời giải chi tiết

Câu 1:

Phương pháp giải:

Bước 1: Thực hiện nhân đơn thức với đa thức.

Bước 2: Cộng trừ các đơn thức đồng dạng và rút gọn

Lời giải:

\(a)\,\,2{x^2}\left( {x - 2} \right) + 3x\left( {{x^2} - x - 2} \right) \)\(- 5\left( {3 - {x^2}} \right)\)

\( = 2{x^3} - 4{x^2} + 3{x^3} - 3{x^2}\)\( - 6x - 15 + 5{x^2}\)

\( = \left( {2{x^3} + 3{x^3}} \right) \)\(+ \left( { - 4{x^2} - 3{x^2} + 5{x^2}} \right) - 6x - 15\)

\( = 5{x^3} - 2{x^2} - 6x - 15\)

\(b)\,\,\left( {x - 1} \right)\left( {x - 3} \right) - \left( {4 - x} \right)\left( {2x + 1} \right) \)\(- 3{x^2} + 2x - 5\)

\(= {x^2} - 3x - x + 3 - \left( {8x + 4 - 2{x^2} - x} \right) \)\(- 3{x^2} + 2x - 5\)

\( = {x^2} - 3x - x + 3 - 8x - 4 + 2{x^2} \)\(+ x - 3{x^2} + 2x - 5\)

\( =  - 9x - 6\)

Câu 2:

Phương pháp giải:

a) Áp dụng hằng đẳng thức: \({A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\)

b) Áp dụng quy tắc: Nhân đa thức với đa thức và các hằng đẳng thức sau đó thực hiện cộng trừ các đơn thức đồng dạng và rút gọn

Hằng đẳng thức:

\(\begin{array}{l}{A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\\{\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\end{array}\)

Lời giải:

\(\begin{array}{l}a)\,\,\left( {x - y} \right)\left( {x + y} \right)\left( {{x^2} + {y^2}} \right)\left( {{x^4} + {y^4}} \right)\\ = \left[ {\left( {x - y} \right)\left( {x + y} \right)} \right]\left( {{x^2} + {y^2}} \right)\left( {{x^4} + {y^4}} \right)\\ = \left( {{x^2} - {y^2}} \right)\left( {{x^2} + {y^2}} \right)\left( {{x^4} + {y^4}} \right)\\ = \left[ {\left( {{x^2} - {y^2}} \right)\left( {{x^2} + {y^2}} \right)} \right]\left( {{x^4} + {y^4}} \right)\\ = \left( {{x^4} - {y^4}} \right)\left( {{x^4} + {y^4}} \right)\\ = {x^8} - {y^8}\end{array}\)

\(b)\,\,\left( {x + 2} \right)\left( {{x^2} + 2x + 4} \right) - {\left( {x - 2} \right)^3} \)\(- 6\left( {x - 1} \right)\left( {x + 1} \right)\)

\(= {x^3} + 2{x^2} + 4x + 2{x^2} + 4x + 8 \)\(- \left( {{x^3} - 3{x^2}.2 + 3x{{.2}^2} - {2^3}} \right) \)\(- 6\left( {{x^2} - {1^2}} \right)\)

\( = {x^3} + 2{x^2} + 4x + 2{x^2} + 4x + 8 \)\(- {x^3} + 6{x^2} - 12x + 8 - 6{x^2} + 6\)

\( = 4{x^2} - 4x + 22\)

Câu 3:

Phương pháp giải:

a) Sử dụng phương pháp nhóm và phương pháp đặt nhân tử chung.

b) Sử dụng phương pháp hằng đẳng thức.

Áp dụng các hằng đẳng thức:

\(\begin{array}{l}{\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\\{A^2} - {B^2} = \left( {A - B} \right)\left( {A + B} \right)\end{array}\)

c) Sử dụng phương pháp tách, nhóm, hằng đẳng thức và đặt nhân tử chung.

Lời giải:

\(\begin{array}{l}a)\,\,3{x^3} - 3{x^2}y - 6{x^2} + 6xy\\ = \left( {3{x^3} - 3{x^2}y} \right) + \left( { - 6{x^2} + 6xy} \right)\\ = 3{x^2}\left( {x - y} \right) - 6x\left( {x - y} \right)\\ = 3x\left( {x - y} \right)\left( {x - 2} \right)\end{array}\)

\(b)\,\,4{x^2} - 20xy + 25 - {\left( {3x - 2} \right)^2}\)

\( = \left( {4{x^2} - 20xy + 25} \right) - {\left( {3x - 2} \right)^2}\)

\( = \left[ {{{\left( {2x} \right)}^2} - 2.2x.5 + {5^2}} \right] \)\(- {\left( {3x - 2} \right)^2}\)

\( = {\left( {2x - 5} \right)^2} - {\left( {3x - 2} \right)^2}\)

\( = \left[ {\left( {2x - 5} \right) - \left( {3x - 2} \right)} \right]\)\(.\left[ {\left( {2x - 5} \right) + \left( {3x - 2} \right)} \right]\)

\( = \left( {2x - 5 - 3x + 2} \right)\)\(.\left( {2x - 5 + 3x - 2} \right)\)

\(= \left( { - x - 3} \right)\left( {5x - 7} \right)\)

\(\begin{array}{l} c)\,\,{x^2} - 6x + 5 + {\left( {x - 5} \right)^2}\\ = {x^2} - x - 5x + 5 + {\left( {x - 5} \right)^2}\\ = \left( {{x^2} - x} \right) + \left( { - 5x + 5} \right) + {\left( {x - 5} \right)^2}\\ = x\left( {x - 1} \right) - 5\left( {x - 1} \right) + {\left( {x - 5} \right)^2}\\ = \left( {x - 1} \right)\left( {x - 5} \right) + {\left( {x - 5} \right)^2}\\ = \left( {x - 5} \right)\left( {x - 1 + x - 5} \right)\\ = \left( {x - 5} \right)\left( {2x - 6} \right)\\ = 2\left( {x - 5} \right)\left( {x - 3} \right)\end{array}\)

Câu 4:

Phương pháp giải:

Áp dụng quy tắc chia đa thức một biến đã sắp xếp.

Lời giải:

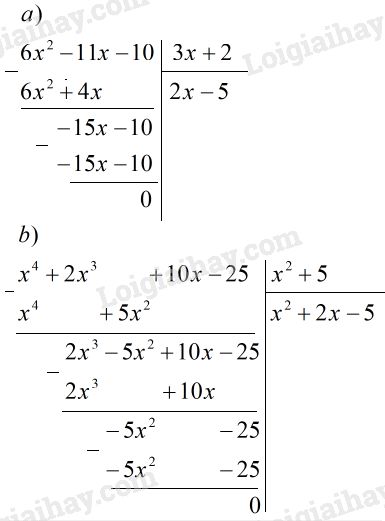
Loigiaihay.com