-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương 1 - Phép nhân và chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng, hình chóp đều
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 8 trang 98 Vở bài tập toán 8 tập 1
Giải bài 8 trang 98 VBT toán 8 tập 1. Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Đề bài
Cho hình thang cân \(ABCD \;(AB // CD)\), \(E\) là giao điểm của hai đường chéo. Chứng minh rằng \(EA = EB, EC = ED.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Hình thang cân có hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
- Hai tam giác bằng nhau có các góc tương ứng bằng nhau
- Tam giác cân có hai cạnh bên bằng nhau, hai góc đáy bằng nhau.
Lời giải chi tiết
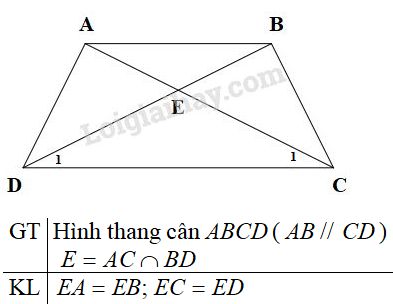
\(\Delta ACD\) và \(\Delta BDC\) có:
+) \(AD = BC\) (vì \(ABCD\) là hình thang cân)
+) \(AC = BD\) (vì \(ABCD\) là hình thang cân)
+) \(DC\) cạnh chung
Do đó \(∆ACD = ∆BDC\) (c.c.c)
Suy ra \(\widehat{C_{1}}=\widehat{D_{1}}\) (\(2\) góc tương ứng)
Tam giác \( ECD\) có \(\widehat{C_{1}}=\widehat{D_{1}}\) nên là tam giác cân, suy ra \( EC = ED\).
Chứng minh tương tự \( EA = EB\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 9 trang 98 Vở bài tập toán 8 tập 1
- Bài 10 trang 99 Vở bài tập toán 8 tập 1
- Bài 11 trang 100 Vở bài tập toán 8 tập 1
- Bài 12 trang 100 Vở bài tập toán 8 tập 1
- Bài 7 trang 97 Vở bài tập toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
