Bài 3. Hình thang cân

Bài 10 trang 99 Vở bài tập toán 8 tập 1

Giải bài 10 trang 99 VBT toán 8 tập 1. Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Đề bài

Cho tam giác \(ABC\) cân tại \(A\), các đường phân giác \(BD, CE\) (\(D ∈ AC, E ∈ AB\)). Chứng minh rằng \(BEDC\) là hình thang cân có đáy nhỏ bằng cạnh bên.

Phương pháp giải - Xem chi tiết

Sử dụng:

- Hai tam giác bằng nhau có các cạnh tương ứng bằng nhau.

- Tam giác cân có hai cạnh bên bằng nhau hai góc đáy bằng nhau.

- Hai đường thẳng song song khi có cặp góc đồng vị bằng nhau.

- Hình thang là tứ giác có hai cạnh đối song song.

- Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau.

Lời giải chi tiết

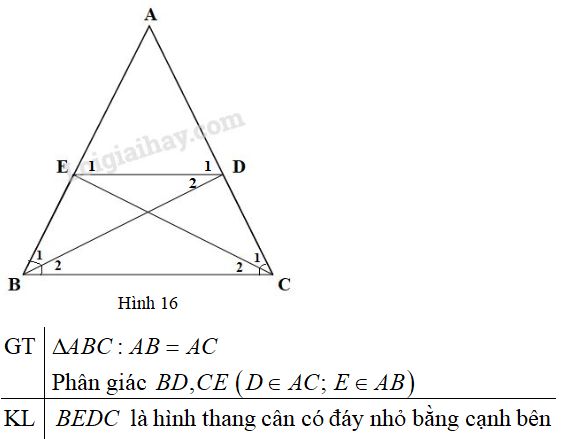
\(∆ABD\) và \(∆ACE\) có:

\(AB = AC\) (vì tam giác \(ABC\) cân tại \(A\))

\(\widehat{A}\) chung

\(\widehat {{B_1}} = \widehat {{C_1}}\) (vì \(\widehat {{B_1}} = \dfrac{1}{2}\widehat B,\,\widehat {{C_1}} = \dfrac{1}{2}\widehat C\,\,\text{và}\,\,\widehat B = \widehat C\))

Do đó \( \Delta ABD = \Delta ACE{\rm{ }}\left( {g.c.g} \right) \) suy ra \( A{\rm{D}} = A{\rm{E}}\)

Tam giác \( ABC\) cân nên \(\widehat B = \widehat C = \left( {{{180}^o} - \widehat A} \right):2\) (1)

Tam giác \(ADE\) cân nên \(\widehat {{E_1}} = \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right):2\) (2)

Từ (1) và (2) suy ra \(\widehat B = \widehat {{E_1}}\), hai góc này ở vị trí đồng vị nên \(ED//BC\).

Vậy \(BEDC\) là hình thang, lại có \(\widehat B = \widehat C \) nên là hình thang cân.

Do \(ED//BC\) nên \(\widehat {{D_2}} = \widehat {{B_2}}\) (SLT), lại có \(\widehat {{B_1}} = \widehat {{B_2}}\) nên \(\widehat {{D_2}} = \widehat {{B_1}}\), suy ra \(\Delta BDE\) cân, do đó \(EB = ED\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 23 phiếu

Bài tiếp theo

Bài 11 trang 100 Vở bài tập toán 8 tập 1
Giải bài 11 trang 100 VBT toán 8 tập 1. Hình thang ABCD (AB // CD) có góc ACD= góc BDC. Chứng minh rằng ABCD là hình thang cân.
Bài 12 trang 100 Vở bài tập toán 8 tập 1
Giải bài 12 trang 100 VBT toán 8 tập 1. Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB//CD) có AC = BD...
Bài 9 trang 98 Vở bài tập toán 8 tập 1
Giải bài 9 trang 98 VBT toán 8 tập 1. Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE...
Bài 8 trang 98 Vở bài tập toán 8 tập 1
Giải bài 8 trang 98 VBT toán 8 tập 1. Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
Bài 7 trang 97 Vở bài tập toán 8 tập 1
Giải bài 7 trang 97 VBT toán 8 tập 1. Cho hình thang cân ABCD ( AB // CD, AB < CD). Kẻ đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
Phần câu hỏi bài 3 trang 97 Vở bài tập toán 8 tập 1
Giải phần câu hỏi bài 3 trang 97 VBT toán 8 tập 1. Khoanh tròn vào chữ cái trước câu trả lời đúng. Một hình thang cân có hiệu của hai góc bằng 40^o. Hai góc đó bằng...