-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 4.4 trang 199 SBT giải tích 12
Giải bài 4.4 trang 199 sách bài tập giải tích 12. Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình...
Đề bài
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình dưới đây?
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ và nhận xét phần thực và phần ảo của số phức \(z\).
Lời giải chi tiết
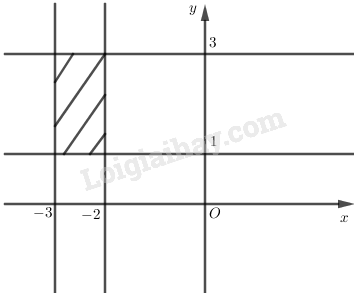
a) Từ hình vẽ ta thấy số phức thỏa mãn phần thực của \(z\) thuộc đoạn \([-3; -2] \) trên trục \(Ox\); phần ảo của \(z\) thuộc đoạn \([1; 3] \) trên trục \(Oy\).
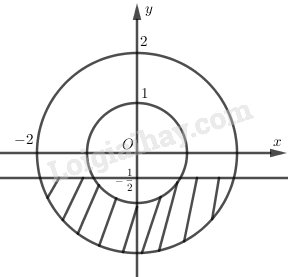
b) Phần gạch chéo được giới hạn bởi hai đường tròn \({x^2} + {y^2} = 1\) và \({x^2} + {y^2} = 4\) và phần ảo \(y \le - \dfrac{1}{2}\).
Vậy số phức \(z\) thỏa mãn phần ảo của \(z\) nhỏ hơn hoặc bằng \( - \dfrac{1}{2},\)\(1 \le \left| z \right| \le 2\)
Bình luận
Chia sẻ
- Bài 4.5 trang 199 SBT giải tích 12
- Bài 4.6 trang 199 SBT giải tích 12
- Bài 4.7 trang 200 SBT giải tích 12
- Bài 4.3 trang 199 SBT giải tích 12
- Bài 4.2 trang 198 SBT giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Tham Gia Group Dành Cho 2K7 luyện thi Tn THPT - ĐGNL - ĐGTD
