-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ - SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Lũy thừa của một số hữu tỉ
- Bài 6. Lũy thừa của một số hữu tỉ ( tiếp theo)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ - Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơclit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC . CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Ôn tập chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 41 trang 88 Vở bài tập toán 7 tập 2
Giải bài 41 trang 88 VBT toán 7 tập 2. Chứng minh định lí : Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là ...
Đề bài
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.
Phương pháp giải - Xem chi tiết
Gợi ý : Kéo dài \(AD\) một đoạn \(D{A_1}\) sao cho \(D{A_1}= AD.\)
Lời giải chi tiết
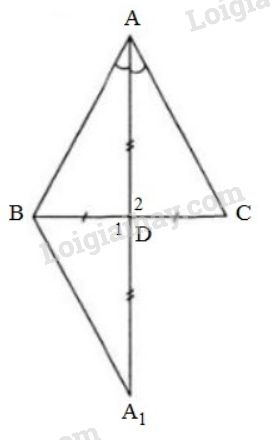
Giả sử tam giác \(ABC\) có đường trung tuyến \(AD\) đồng thời là đường phân giác. Trên tia \(AD\) lấy điểm \({A_1}\) sao cho \(D{A_1}= AD.\)
Ta sẽ chứng minh tam giác \(ABC\) cân tại \(A\).
Xét hai tam giác \(ADC\) và \({A_1}DB\). Ta có \(DC = DB\) (vì \(AD\) là đường trung tuyến của tam giác \(ABC\)), \(AD = D{A_1}\) (theo cách lấy điểm \({A_1}\)), \( \widehat{BDA_1} = \widehat{CDA}\) (hai góc đối đỉnh). Vậy \(∆ADC = ∆{A_1}DB\) (c.g.c).
Suy ra \( \widehat{DAC} = \widehat{DA_1B}\) (1), \(AC=BA_1\) (2).
Xét tam giác \(BA{A_1}\). Ta có \( \widehat{BAA_1} = \widehat{BA_1A}\) (vì theo (1) \( \widehat{BA_1D} = \widehat{DAC}\) và do \(AD\) là đường phân giác nên \( \widehat{DAC} = \widehat{BAA_1}\)). Suy ra tam giác \(BA{A_1}\) cân tại \(B\), do đó \(AB = {A_1}B\) (3)
Từ (2) và (3) suy ra \(AB = AC\).
Vậy \(∆ABC\) cân tại \(A.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 40 trang 87 Vở bài tập toán 7 tập 2
- Bài 39 trang 87 Vở bài tập toán 7 tập 2
- Bài 38 trang 86 Vở bài tập toán 7 tập 2
- Bài 37 trang 85 Vở bài tập toán 7 tập 2
- Bài 36 trang 85 Vở bài tập toán 7 tập 2
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
