-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 2.2 trang 47 SBT hình học 12.
Giải bài 2.2 trang 47 sách bài tập hình học 12. Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh bằng a.
Một hình nón tròn xoay có thiết diện qua trục là một tam giác vuông cân có cạnh bằng \(a\).
LG a
Tính diện tích toàn phần và thể tích hình nón đó.
Phương pháp giải:
Sử dụng các công thức \({S_{tp}} = {S_{xq}} + {S_d} = \pi rl + \pi {r^2}\) và \(V = \dfrac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
Thiết diện qua trục của hình nón là tam giác vuông cân cạnh \(a\) nên hình nón có đường sinh \(l=a\), có đường kính đáy \(a\sqrt 2 \) nên bán kính đáy \(r = \dfrac{{a\sqrt 2 }}{2}\), và có chiều cao \(h = r = \dfrac{{a\sqrt 2 }}{2}\)
Gọi \({S_{xq}}\) là diện tích xung quanh của hình nón, ta có: \({S_{xq}} = \pi rl = \pi \dfrac{{a\sqrt 2 }}{2}.a = \dfrac{{\pi {a^2}\sqrt 2 }}{2}\)
Gọi \(S\) là diện tích đáy của hình nón, ta có \({S_d} = \pi {r^2} = \dfrac{{\pi {a^2}}}{2}\)
Vậy diện tích toàn phần của hình nón đã cho là:
\({S_{tp}} = {S_{xq}} + {S_d}\)\( = \dfrac{1}{2}\pi {a^2}\sqrt 2 + \dfrac{1}{2}\pi {a^2}\) \( = \dfrac{1}{2}\pi {a^2}\left( {\sqrt 2 + 1} \right)\)
Hình nón có thể tích là: \(V = \dfrac{1}{3}\pi {r^2}h\)\( = \dfrac{1}{3}\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}.\dfrac{{a\sqrt 2 }}{2}\) \( = \dfrac{1}{{12}}\pi {a^3}\sqrt 2 \)
LG b
Một mặt phẳng đi qua đỉnh tạo với mặt phẳng đáy một góc \({60^0}\). Tính diện tích thiết diện được tạo nên.
Phương pháp giải:
Xác định góc \({60^0}\) (góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng cùng vuông góc giao tuyến).
Tính diện tích theo công thức \(S = \dfrac{1}{2}dh\) với \(d\) là độ dài cạnh đáy tam giác, \(h\) là chiều cao
Lời giải chi tiết:
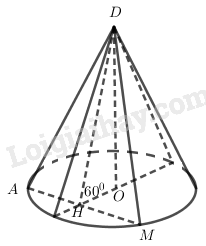
Xét mặt phẳng \((DAM) \) đi qua đỉnh \(D\) tạo với mặt phẳng đáy một góc \({60^0}\), cắt đường tròn đáy tại hai điểm \(A\) và \(M\).
Từ tâm \(O\) của đường tròn đáy ta vẽ \(OH \bot AM\), do vậy \(H\) là trung điểm của đoạn \(AM\). Ta có \(AM \bot (DOH)\) vì \(AM \bot OH\) và \(AM \bot DO\).
Vậy \(\widehat {DHO} = {60^0}\) và \(\sin {60^0} = \dfrac{{DO}}{{DH}}\) hay \(DH = \dfrac{{DO}}{{\sin {{60}^0}}} = \dfrac{{a\sqrt 2 }}{2}:\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }}\)
Gọi \({S_{\Delta DAM}}\) là diện tích thiết diện cần tìm, ta có: \({S_{\Delta DAM}} = \dfrac{1}{2}AM.DH = AH.DH\)
Mà \(A{H^2} = D{A^2} - D{H^2}\)\( = {a^2} - \dfrac{{2{a^2}}}{3} = \dfrac{{{a^2}}}{3}\) \( \Rightarrow AH = \dfrac{a}{{\sqrt 3 }}\)
Vậy \({S_{\Delta DAM}} = AH.DH \) \(= \dfrac{a}{{\sqrt 3 }}.\dfrac{{a\sqrt 2 }}{{\sqrt 3 }} = \dfrac{{{a^2}\sqrt 2 }}{3}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2.3 trang 47 SBT hình học 12
- Bài 2.4 trang 47 SBT hình học 12
- Bài 2.5 trang 47 SBT hình học 12
- Bài 2.6 trang 47 SBT hình học 12
- Bài 2.7 trang 47 SBT hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
