-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: PHÉP NHÂN VÀ CHIA CÁC ĐA THỨC
- Bài 1. Nhân đơn thức với đa thức
- Bài 2. Nhân đa thức với đa thức
- Bài 3. Những hằng đẳng thức đáng nhớ
- Bài 4. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 5. Những hằng đẳng thức đáng nhớ (tiếp)
- Bài 6. Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- Bài 8. Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- Bài 9. Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- Bài 10. Chia đơn thức cho đơn thức
- Bài 11. Chia đa thức cho đơn thức
- Bài 12. Chia đa thức một biến đã sắp xếp
- Ôn tập chương 1 - Phép nhân và chia các đa thức
-
CHƯƠNG 2: PHÂN THỨC ĐẠI SỐ
- Bài 1. Phân thức đại số
- Bài 2. Tính chất cơ bản của phân thức
- Bài 3. Rút gọn phân thức
- Bài 4. Quy đồng mẫu thức nhiều phân thức
- Bài 5. Phép cộng các phân thức đại số
- Bài 6. Phép trừ các phân thức đại số
- Bài 7. Phép nhân các phân thức đại số
- Bài 8. Phép chia các phân thức đại số
- Bài 9. Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- Ôn tập chương 2 - Phân thức đại số
-
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 1
-
CHƯƠNG 1: TỨ GIÁC
- Bài 1. Tứ giác
- Bài 2. Hình thang
- Bài 3. Hình thang cân
- Bài 4. Đường trung bình của tam giác, của hình thang
- Bài 5. Dựng hình bằng thước và compa. Dựng hình thang
- Bài 6. Đối xứng trục
- Bài 7. Hình bình hành
- Bài 8. Đối xứng tâm
- Bài 9. Hình chữ nhật
- Bài 10. Đường thẳng song song với một đường thẳng cho trước
- Bài 11. Hình thoi
- Bài 12. Hình vuông
- Ôn tập chương 1 - Tứ giác
-
CHƯƠNG 2: ĐA GIÁC - DIỆN TÍCH ĐA GIÁC
-
-
PHẦN ĐẠI SỐ - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
PHẦN HÌNH HỌC - VỞ BÀI TẬP TOÁN 8 TẬP 2
-
CHƯƠNG 3: TAM GIÁC ĐỒNG DẠNG
- Bài 1. Định lí Ta - lét trong tam giác
- Bài 2. Định lí đảo và hệ quả của định lí Ta - lét
- Bài 3. Tính chất đường phân giác của tam giác
- Bài 4. Khái niệm hai tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
- Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
- Bài 7. Trường hợp đồng dạng thứ ba (g.g)
- Bài 8. Các trường hợp đồng dạng của tam giác vuông
- Bài 9. Ứng dụng thực tế của tam giác đồng dạng
- Ôn tập chương 3 - Tam giác đồng dạng
-
CHƯƠNG 4: HÌNH LĂNG TRỤ ĐỨNG. HÌNH CHÓP ĐỀU
- Bài 1. Hình hộp chữ nhật
- Bài 2. Hình hộp chữ nhật (tiếp)
- Bài 3. Thể tích của hình hộp chữ nhật
- Bài 4. Hình lăng trụ đứng
- Bài 5. Diện tích xung quanh của hình lăng trụ đứng
- Bài 6. Thể tích của hình lăng trụ đứng
- Bài 7. Hình chóp đều và hình chóp cụt đều
- Bài 8. Diện tích xung quanh của hình chóp đều
- Bài 9. Thể tích của hình chóp đều
- Ôn tập chương 4 - Hình lăng trụ đứng, hình chóp đều
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 17 trang 152 Vở bài tập toán 8 tập 1
Giải bài 17 trang 152 vở bài tập toán 8 tập 1. Tính diện tích của một tam giác đều có cạnh là a.
Đề bài
Tính diện tích của tam giác đều có cạnh bằng \(a\).
Phương pháp giải - Xem chi tiết
Sử dụng:
- Tam giác đều là tam giác có ba cạnh bằng nhau.
- Định lí Pytago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
Lời giải chi tiết
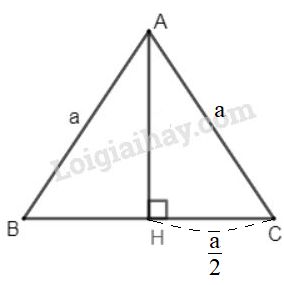
Xét \(\Delta ABC\) đều cạnh \(a\). Kẻ \(AH\bot BC\).
Ta có \(BH=HC= \dfrac{a}{2}\)
Áp dụng định lý Pytago vào \(\Delta ABH\), ta có
\(A{H^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2} \), suy ra \(AH = \dfrac{{a\sqrt 3 }}{2}\)
Vậy \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.\dfrac{{a\sqrt 3 }}{2}.a \)\(\,= \dfrac{{{a^2}\sqrt 3 }}{4}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 16 trang 151 Vở bài tập toán 8 tập 1
- Bài 15 trang 151 Vở bài tập toán 8 tập 1
- Bài 14 trang 150 Vở bài tập toán 8 tập 1
- Bài 13 trang 150 Vở bài tập toán 8 tập 1
- Bài 12 trang 149 Vở bài tập toán 8 tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
