Bài 1.14 trang 18 SBT hình học 12
Giải bài 1.14 trang 18 sách bài tập hình học 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD.
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,BC = 2a,AA' = a\). Lấy điểm \(M\) trên cạnh \(AD\) sao cho \(AM = 3MD\).
LG a
Tính thể tích khối chóp \(M.AB'C\)
Phương pháp giải:
- Đổi vị trí đỉnh và đáy của khối chóp, đưa về khối chóp có chiều cao và đáy dễ tính toán.
- Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\).
Giải chi tiết:
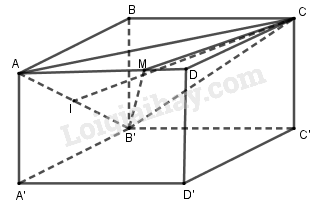
Ta có: \({V_{M.AB'C}} = {V_{B'.ACM}}\).
\({S_{AMC}} = \dfrac{3}{4}{S_{ADC}} = \dfrac{3}{4}.\dfrac{1}{2}.2{a^2} = \dfrac{{3{a^2}}}{4}\)
Do đó \({V_{M.AB'C}} = {V_{B'.ACM}} = \dfrac{1}{3}B'B.{S_{AMC}}\)\( = \dfrac{1}{3}.\dfrac{{3{a^2}}}{4}.a = \dfrac{{{a^3}}}{4}\)
LG b
Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {AB'C} \right)\).
Phương pháp giải:
- Tính diện tích tam giác \(AB'C\).
- Dựa vào thể tích và diện tích của khối chóp \(M.AB'C\) suy ra khoảng cách theo công thức \(h = \dfrac{{3V}}{S}\).
Giải chi tiết:
Gọi \(h\) là khoảng cách từ \(M\) đến mặt phẳng \(\left( {AB'C} \right)\)
Khi đó \({V_{M.AB'C}} = \dfrac{1}{3}{S_{AB'C}}.h = \dfrac{{{a^3}}}{4}\)
Vì \(A{C^2} = {\rm{ }}B'{C^2} = 5{a^2}\) nên tam giác \(ACB'\) cân tại \(C\). Do đó, đường trung tuyến \(CI\) của tam giác \(ACB'\) cũng là đường cao.
Ta có: \(C{I^2} = {\rm{ }}C{A^2}-{\rm{ }}A{I^2}\)\( = {\rm{ }}5{a^2} - {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}\) \( = 5{a^2} - \dfrac{{{a^2}}}{2} = \dfrac{{9{a^2}}}{2}\)
Do đó \(CI = \dfrac{{3a}}{{\sqrt 2 }}\)\( \Rightarrow {S_{AB'C}} = \dfrac{1}{2}.\dfrac{{3a}}{{\sqrt 2 }}.a\sqrt 2 = \dfrac{{3{a^2}}}{2}\)
\( \Rightarrow h = \dfrac{{3V}}{S} = \dfrac{{3{a^3}}}{4}:\dfrac{{3{a^2}}}{2} = \dfrac{a}{2}\).
Loigiaihay.com













Danh sách bình luận