Bài 1.11 trang 18 SBT hình học 12

Giải bài 1.11 trang 18 sách bài tập hình học 12. Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC = 5a, BC = 6a và các mặt bên tạo với đáy một góc 600.Hãy tính thể tích của khối chóp đó.

Đề bài

Cho khối chóp \(S.ABC\) có đáy là tam giác cân, \(AB = AC = 5a,BC = 6a\) và các mặt bên tạo với đáy một góc \({60^0}\). Hãy tính thể tích của khối chóp đó.

Phương pháp giải - Xem chi tiết

- Dựng hình chiếu của \(S\) trên mặt đáy, từ đó xác định góc giữa các mặt bên và mặt đáy.

- Tính diện tích đáy, chiều cao dựa vào các kiến thức hình học đã biết.

- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).

Lời giải chi tiết

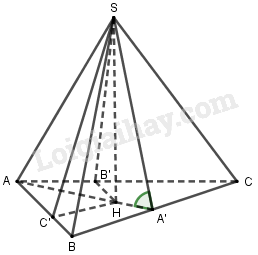
Kẻ \(SH \bot \left( {ABC} \right)\) và \(HA',HB',HC'\) lần lượt vuông góc với \(BC,CA,AB\). Theo định lí ba đường vuông góc ta có \(SA' \bot BC,SB' \bot CA,SC' \bot AB\)

Từ đó suy ra \(\widehat {SA'H} = \widehat {SB'H} = \widehat {SC'H} = {60^0}\).

\( \Rightarrow \Delta SHA' = \Delta SHB' = \Delta SHC'\)\( \Rightarrow HA' = HB' = HC'\)

Do đó \(H\) là tâm đường tròn nội tiếp tam giác \(ABC\). Do tam giác cân ở \(A\) nên \(AH\) vừa là đường phân giác, vừa là đường cao, vừa là đường trung tuyến.

\( \Rightarrow A,H,A'\) thẳng hàng và \(A'\) là trung điểm của \(BC\).

Tam giác \(\Delta AA'B\) vuông tại \(A'\) nên \(AA{'^2} = A{B^2}-BA{'^2}\) \( = 25{a^2}-9{a^2} = 16{a^2}\) \( \Rightarrow AA' = 4a\)

Gọi \(p\) là nửa chu vi của tam giác \(ABC\), \(r\) là bán kính đường tròn nội tiếp tam giác \(r = HA'\).

Ta có: \(p = \frac{{AB + BC + CA}}{2}\) \( = \frac{{5a + 6a + 5a}}{2} = 8a\)

\({S_{ABC}} = \frac{1}{2}AA'.BC = \frac{1}{2}.4a.6a = 12{a^2}\)

Lại có \({S_{ABC}} = pr \Rightarrow 12{a^2} = 8a.r\) \( \Rightarrow r = \dfrac{3}{2}a\)

Tam giác SHA' vuông tại H có \( SH = HA'.\tan {60^0} \) \(= \dfrac{{3a}}{2}\sqrt 3 = \dfrac{{3\sqrt 3 }}{2}a\)

Thể tích khối chóp là \(V = \frac{1}{3}{S_{ABC}}.SH\) \(= \dfrac{1}{3}.12{a^2}.\dfrac{{3\sqrt 3 }}{2}a = 6\sqrt 3 {a^3}\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 1.12 trang 18 SBT hình học 12
Giải bài 1.12 trang 18 sách bài tập hình học 12. Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c.
Bài 1.13 trang 18 SBT hình học 12
Giải bài 1.13 trang 18 sách bài tập hình học 12. Chứng minh rằng tổng các khoảng cách từ một điểm bất kì trong một tứ diện đều đến các mặt phẳng của nó là một số không đổi.
Bài 1.14 trang 18 SBT hình học 12
Giải bài 1.14 trang 18 sách bài tập hình học 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD.
Bài 1.15 trang 19 SBT hình học 12
Giải bài 1.15 trang 19 sách bài tập hình học 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
Bài 1.16 trang 19 SBT hình học 12
Giải bài 1.16 trang 19 sách bài tập hình học 12. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho.
Bài 1.17 trang 19 SBT hình học 12
Giải bài 1.17 trang 19 sách bài tập hình học 12. Cho hình hộp ABCD.A’B’C’D’. Gọi E và F lần lượt là trung điểm của B’C’ và C’D’.
Bài 1.10 trang 18 SBT hình học 12
Giải bài 1.10 trang 18 sách bài tập hình học 12. Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 600. Hãy tính thể tích của khối chóp đó.