Bài 3. Thể tích của hình hộp chữ nhật

Bài 10 trang 118 Vở bài tập toán 8 tập 2

Giải bài 10 trang 118 VBT toán 8 tập 2. A, B, C và D là những đỉnh của hình hộp chữ nhật cho ở hình 70...

Đề bài

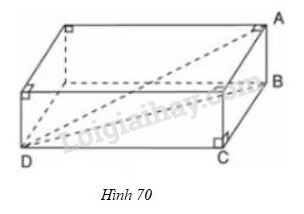
\(A,\, B,\, C \) và \(D\) là những đỉnh của hình hộp chữ nhật cho ở hình 70.

Hãy điền số thích hợp vào các ô trống ở bảng sau:

AB	6	13	14
BC	15	16		34
CD	42		70	62
DA		45	75	75

Kết quả bài 10 minh họa công thức quan trọng sau:

\(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

Phương pháp giải - Xem chi tiết

- Áp dụng định lý Py-ta-go trong tam giác vuông để chứng minh công thức:

\(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

- Áp dụng công thức bên trên để tìm độ dài các đoạn thẳng chưa biết.

Lời giải chi tiết

Trước hết ta chứng minh hệ thức sau: \(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

Ta có : \( \triangle BCD\) vuông tại \( C \Rightarrow BD^2 = DC^2 + BC^2\)

\( \triangle ABD\) vuông tại \(B \Rightarrow AD^2 = BD^2 + AB^2\)

\( \Rightarrow AD^2 = DC^2 +BC^2 + AB^2 \)

Suy ra: \(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

Áp dụng hệ thức này ta sẽ tính được độ dài một cạnh khi biết ba độ dài kia.

Cột 1: \(AB=6,BC=15, CD=42\)

\(DA = \sqrt {{6^2} + {{15}^2} + {{42}^2}} = \sqrt {2025} \)\(\,= 45\)

Cột 2: \(AB=13,BC=16,DA=45\)

\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow C{D^2} = D{A^2} - A{B^2} - B{C^2} \cr
& \Rightarrow CD = \sqrt {D{A^2} - A{B^2} - B{C^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{45}^2} - {{16}^2} - {{13}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {1600} = 40 \cr} \)

Cột 3: \(AB=14,CD=70,DA=75\)

\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow B{C^2} = D{A^2} - A{B^2} - C{D^2} \cr
& \Rightarrow BC = \sqrt {D{A^2} - A{B^2} - C{D^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{75}^2} - {{14}^2} - {{70}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {529} = 23 \cr} \)

Cột 4: \(BC=34,CD=62,DA=75\)

\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow A{B^2} = D{A^2} - B{C^2} - C{D^2} \cr
& \Rightarrow AB = \sqrt {D{A^2} - B{C^2} - C{D^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{75}^2} - {{34}^2} - {{62}^2}} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {625} = 25 \cr} \)

Do đó ta có kết quả như bảng dưới đây:

AB	6	13	14	25
BC	15	16	23	34
CD	42	40	70	62
DA	45	45	75	75

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài tiếp theo

Bài 11 trang 119 Vở bài tập toán 8 tập 2
Giải bài 11 trang 119 VBT toán 8 tập 2. Viết công thức tính thể tích của hình hộp chữ nhật ABCD.MNPQ (h71)...
Bài 12 trang 119 Vở bài tập toán 8 tập 2
Giải bài 12 trang 119 VBT toán 8 tập 2. Một bể nước hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không có nước...
Bài 13 trang 120 Vở bài tập toán 8 tập 2
Giải bài 13 trang 120 VBT toán 8 tập 2. Một cái thùng hình lập phương, cạnh...
Bài 14 trang 121 Vở bài tập toán 8 tập 2
Giải bài 14 trang 121 VBT toán 8 tập 2. Cho hình hộp chữ nhật ABCD.EFGH (h.74):...
Bài 9 trang 118 Vở bài tập toán 8 tập 2
Giải bài 9 trang 118 VBT toán 8 tập 2. Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với...
Phần câu hỏi bài 3 trang 117 Vở bài tập toán 8 tập 2
Giải phần câu hỏi bài 3 trang 117 VBT toán 8 tập 2. Đúng ghi Đ, sai ghi S vào ô trống trong mỗi mệnh đề sau:...