 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Đề kiểm tra 15 phút – Chương IV – Giải tích 12
Đề kiểm tra 15 phút – Chương IV – Giải tích 12
Đề kiểm tra 15 phút – Đề số 5 – Chương IV - Giải tích 12
Đáp án và lời giải chi tiết Đề kiểm tra 15 phút – Đề số 5 – Chương IV - Giải tích 12.
Đề bài
Câu 1. Phần thực của số phức z = -2 +3i là
A. 2 B. -2
C. 3 D. -3.
Câu 2. Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z| = 2\) là:
A. Hai đường thẳng .
B. Đường tròn đường kính bằng 8.
C. Đường tròn bán kính bằng 2.
D. Hình tròn bán kính bằng 2.
Câu 3. Căn bậc hai của số phức khác 0 là;
A. Hai số phức liên hợp.
B. Hai số phức bằng nhau.
C. Hai số phức có cùng phần ảo.
D. Hai số phức đối nhau.
Câu 4. Cho các số phức \({z_1} = 4 + 3i\,,\,\,{z_2} = - 4 + 3i\,,\,\,{z_3} = {z_1}.{z_2}\).Lực chọn phương án đúng
A. \(|{z_3}| = 25\).
B. \(\overline {{z_1} + {z_2}} = {z_1} + {z_2}\).
C. \(\overline {{z_1}} = \overline {\overline {{z_2}} } \).
D. \({z_3} = |{z_1}{|^2}\).
Câu 5. Cho phương trình \(5 - 2ix = \left( {3 + 4i} \right)\left( {1 - 3i} \right)\). Nghiệm của phương trình trên tập số phức là :
A. \(x = \dfrac{5}{2} - 5i\).
B. \(x = \dfrac{5}{2} + 5i\).
C. \(x = \dfrac{2}{5} + 5i\).
D. \(x = \dfrac{2}{5} - 5i\).
Câu 6. Cho phương trình \({z^2} - 2z + 2 = 0\). Mệnh đề nào sau đây là sai ?
A. Phương trình đã cho không có nghiệm nào là số thuần ảo.
B. Phương trình đã cho có 2 nghiệm phức.
C. Phương trình đã cho không có nghiệm phức.
D. Phương trình đã cho không có nghiệm thực.
Câu 7. Cho số phức z thỏa mãn \(\left( {2 - i} \right)z = 7 - i\). Hỏi điểm biểu diễn của z là điểm nào trong các điểm M, N, P, Q ở hình dưới.
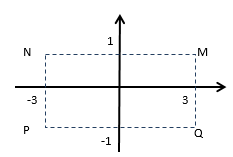
A. Điểm P. B. Điểm M
C. Điểm N D. Điểm Q.
Câu 8. Rút gọn biểu thức sau : \(A + \dfrac{{\left( {1 + i} \right)\left( {2 + i} \right)}}{{2 - i}} + \dfrac{{\left( {1 + i} \right)\left( {2 - i} \right)}}{{2 + i}}\).
A. \(A + \dfrac{6}{5}\left( {1 - i} \right)\).
B. \(A = 1 - i\).
C. \(A = \dfrac{6}{5}\left( {1 + i} \right)\).
D. \(A = 1 + i\).
Câu 9. Phương trình \({z^2} - 4z + 9 = 0\) có hai nghiệm. Giá trị biểu thức \(T = |{z_1}| + |{z_2}|\) bằng :
A. – 6 B. 6
C. 8 D. 12
Câu 10. Tìm mệnh đề sai ?
A. Số phức z = a + bi được biểu diễn bằng điểm M(a; b) trong mặt phẳng phức Oxy.
B. Số phức z = a + bi có số phức liên hợp là \(\overline z = - a + bi\).
C. Số phức z = a + bi = 0 \( \Leftrightarrow \,\,\left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\).
D. Số phức z = a + bi có mô đun là \(\sqrt {{a^2} + {b^2}} \).
Lời giải chi tiết
|
1 |
2 |
3 |
4 |
5 |
|
B |
C |
D |
A |
B |
|
6 |
7 |
8 |
9 |
10 |
|
C |
B |
C |
B |
B |
Lời giải chi tiết
Câu 1.
Số phức \(z = - 2 + 3i\) có phần thực bằng \( - 2\)
Chọn đáp án B.
Câu 2.
Tập hợp các điểm biểu diễn số phức z thỏa mãn \(|z| = 2\) là: Đường tròn bán kính bằng 2.
Chọn đáp án C.
Câu 3.
Căn bậc hai của số phức khác 0 là hai số phức đối nhau.
Chọn đáp án D.
Câu 4.
Ta có: \({z_3} = \left( {4 + 3i} \right)\left( { - 4 + 3i} \right) \)\(\,= - 16 - 9 = - 25\)\( \Rightarrow \left| {{z_3}} \right| = \sqrt {{{\left( { - 25} \right)}^2}} = 25.\)
Chọn phương án A.
Câu 5.
Ta có: \(5 - 2ix = \left( {3 + 4i} \right)\left( {1 - 3i} \right)\)
\(\Leftrightarrow 5 - 2ix = 3 - 9i + 4i + 12\)
\( \Leftrightarrow 5 - 2ix = 15 - 5i\)
\(\Leftrightarrow 10 + \left( {2x - 5} \right)i = 0 \)
\(\Rightarrow x = \dfrac{5}{2}\)
Khi đó \(x = \dfrac{5}{2} + 5i\)
Chọn đáp án B.
Câu 6.
Ta có: \({z^2} - 2z + 2 = 0 \Leftrightarrow x = 1 \pm i\)
+ Phương trình không có nghiệm nào thuần ảo.
+ Phương trình có 2 nghiệm phức.
+ Phương trình đã cho không có nghiệm thực.
Chọn đáp án C.
Câu 7.
Ta có: \(\left( {2 - i} \right)z = 7 - i \)
\(\Leftrightarrow \left( {2 - i} \right)\left( {a + bi} \right) = 7 - i\)
\( \Leftrightarrow 2a + 2bi - ai + b = 7 - i\)
\(\Leftrightarrow 2a + b - 7 - \left( {a - 2b - 1} \right)i = 0\)
\( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 7\\a - 2b = 1\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 1\end{array} \right.\)
Điểm biểu diễn số phức z là điểm M.
Chọn đáp án B.
Câu 8.
\(\begin{array}{l}A = \dfrac{{\left( {1 + i} \right)\left( {2 + i} \right)}}{{2 - i}} + \dfrac{{\left( {1 + i} \right)\left( {2 - i} \right)}}{{2 + i}}\\\,\,\,\,\,\, = \dfrac{{1 + 3i}}{{2 - i}} + \dfrac{{3 + i}}{{2 + i}}\\\,\,\,\,\,\, = \dfrac{{\left( {1 + 3i} \right)\left( {2 + i} \right)}}{{\left( {2 - i} \right)\left( {2 + i} \right)}} + \dfrac{{\left( {3 + i} \right)\left( {2 - i} \right)}}{{\left( {2 - i} \right)\left( {2 + i} \right)}}\\\,\,\,\,\,\, = \dfrac{{ - 1 + 7i}}{5} + \dfrac{{7 - i}}{5} = \dfrac{{6\left( {1 + i} \right)}}{5}\end{array}\)
Chọn đáp án C
Câu 9.
Ta có: \({z^2} - 4z + 9 = 0 \Leftrightarrow x = 2 \pm \sqrt 5 i\)
Khi đó \(T = |{z_1}| + |{z_2}| \)\(\,= \sqrt {{2^2} + {{\left( {\sqrt 5 } \right)}^2}} + \sqrt {{2^2} + {{\left( { - \sqrt 5 } \right)}^2}} \)\(\,= 6\)
Chọn đáp án B.
Câu 10.
Số phức \(z = a + bi\) có số phức liên hợp là \(z = a - bi\)
Chọn đáp án B
Loigiaihay.com












Danh sách bình luận