Đề kiểm tra 15 phút - Đề số 1 - Chương 1 - Giải Tích 12

Câu 1.

Nếu \(f'\left( x \right) > 0,\forall x \in K\) thì hàm số đồng biến trên \(K\).

Chú ý:

Đáp án A không đúng vì nếu \(f'\left( x \right) = 0\) với mọi \(x \in K\) thì hàm số là hàm hằng nên không đồng biến trên \(K\).

Chọn C.

Câu 2.

Ta có \(y' =  - {x^2} + 1\)

\(\Rightarrow y' = 0\)

\(\Leftrightarrow \,\, - {x^2} + 1 = 0\)

\(\Leftrightarrow x =  \pm 1\)

Ta có bảng biến thiên:

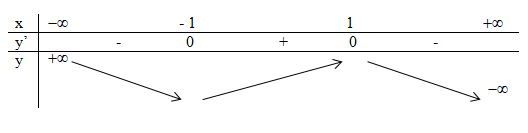
Vậy hàm số đồng biến trên  (- 1; 1).

Chọn đáp án B.

Câu 3.

Ta có

\(y' =  - 3{x^2} + 6x - 3\)\( =  - 3{(x - 1)^2} \le 0,\forall x \in R\)

Vậy hàm số luôn nghịch biến.

Chọn đáp án A.

Câu 4.

Ta có

\(\begin{array}{l}y' = 3{x^2} - 6x,\,\,y' = 0\\ \Leftrightarrow \,\,3{x^2} - 6x = 0\,\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\in [-1;1] \\x = 2\notin [-1;1] \end{array} \right.\\  y(0) = 0,\,\,y( - 1) =  - 4,\,\,y(1) =  - 2.\end{array}\)

Vậy giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2}\)  trên đoạn [-1; 1] là – 4

Chọn đáp án D.

Câu 5.

Ta có \(D = R\backslash \{ 1\} .\)\(y' = \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D\) . 

Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ;1} \right),\left( {1; + \infty } \right)\)

Chọn đáp án A.

Câu 6.

Đồ thị hàm số có đường tiệm cận đứng là x = -1.

Đồ thị hàm số có đường tiệm cận ngang là y = 3.

Vậy tâm đối xứng là giao điểm của hai đường tiệm cận là (-1 ; 3)

Chọn đáp án B.

Câu 7.

\(y' = 4{x^3} - 3{x^2}\,\,,\,y' = 0\)

\(\Leftrightarrow \,\,4{x^3} - 3{x^2} = 0\)

\(\Leftrightarrow \,\left[ \begin{array}{l}x = 0(\text{bội 2})\\x = \dfrac{3}{4}\end{array} \right.\)

Vậy số điểm cực trị của đồ thị hàm số trên là 1 do nghiệm \(x = 0\) là nghiệm kép.

Chọn đáp án A.

Câu 8.

Ta có

\(\begin{array}{l}y' = 3{x^2} - 12x + 12,\,\,y' = 0\\ \Leftrightarrow \,\,3{x^2} - 12x + 12 = 0\\ \Leftrightarrow \,\,3{\left( {x - 2} \right)^2} = 0\\   \Leftrightarrow x = 2\in [0;3]\end{array}\)

\(y(0) = 5,\,\,y(2) = 13,\,\,y(3) = 14\).

Vậy giá trị lớn nhất của hàm số trên đoạn [0 ; 3] là 14

Chọn đáp án A.

Câu 9.

Tiếp tuyến d song song với đường thẳng \(y = -5x -3\) nên có \(k = -5 \).

\(y' = \dfrac{{ - 5}}{{{{\left( {x - 1} \right)}^2}}},\,\,y'({x_0}) =  - 5\\ \Rightarrow \,\dfrac{{ - 5}}{{{{\left( {{x_0} - 1} \right)}^2}}} =  - 5\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 0\end{array} \right.\)

Với \({x_0} = 2\,\, \Rightarrow {y_0} = 7\)

\(\Rightarrow d:\,y =  - 5\left( {x - 2} \right) + 7\) hay \(d:\,\,y =  - 5x + 17\)

Với \({x_0} = 0\,\, \Rightarrow {y_0} =  - 3\)

\(\Rightarrow d:\,y =  - 5\left( {x - 0} \right) - 3 =  - 5x - 3\)  trùng với đường thẳng y= -5x – 3 đề cho.

Vậy chỉ có một đường thẳng thỏa mãn yên cầu đề bài.

Chọn A.

Câu 10.

\(y' = 3{x^2} - 6x - 9,\,\,y' = 0\)

\(\Rightarrow 3{x^2} - 6x - 9 = 0\)

\(\Leftrightarrow \,\left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.\)

Ta có bảng biến thiên:

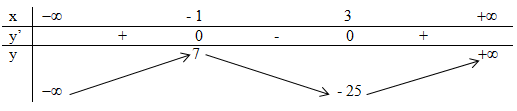
Đồ thị đạt cực tiểu tại x = 3 nên giá trị cực tiểu là y(3)= - 25.

Chọn C.

Loigiaihay.com