-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Bài 2. Khối đa diện lồi và khối đa diện đều
Trả lời câu hỏi 3 trang 17 SGK Hình học 12
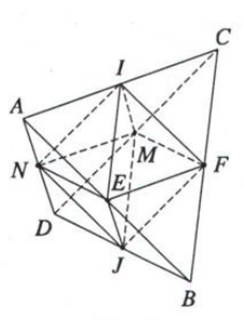
Chứng minh rằng ...
Đề bài
Chứng minh rằng tam giác \(IEF, IFM, IMN, INE, JEF, JFM, JMN\) và \(JNE\) là những tam giác đều cạnh bằng \( \dfrac a 2\)
Video hướng dẫn giải
Lời giải chi tiết
\(ABCD\) là tứ diện đều ⇒ tam giác \(ABC\) đều \(⇒ AB = BC = CA = a\)
\(I, E, F\) lần lượt là trung điểm của các cạnh \(AC, AB, BC\) nên ta có \(IE, IF, EF\) là các đường trung bình của tam giác \(ABC\)
\(\eqalign{
& \Rightarrow IE = {1 \over 2}BC = {1 \over 2}a \cr
& {\rm{IF = }}{1 \over 2}AB = {1 \over 2}a \cr
& {\rm{EF = }}{1 \over 2}AC = {1 \over 2}a \cr} \)
Nên tam giác \(IEF\) là tam giác đều cạnh bằng \(\dfrac a 2\)
Chứng minh tương tự ta có:\(IFM, IMN, INE, JEF, JFM, JMN\) và \(JNE\) là những tam giác đều cạnh bằng \(\dfrac a 2\)
Loigiaihay.com
Bình luận
Chia sẻ
- Trả lời câu hỏi 4 trang 18 SGK Hình học 12
- Giải bài 1 trang 18 SGK Hình học 12
- Giải bài 2 trang 18 SGK Hình học 12
- Giải bài 3 trang 18 SGK Hình học 12
- Giải bài 4 trang 18 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
