-
GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
- Bài 1. Tính đơn điệu của hàm số
- Bài 2. Cực trị của hàm số
- Bài 3. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Bài 4. Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5. Đường tiệm cận của đồ thị hàm số
- Bài 6. Khảo sát sự biến thiên và vẽ đồ thị của một hàm số đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị hàm số của một số hàm phân thức hữu tỉ
- Bài 8. Một số bài toán thường gặp về đồ thị
- Câu hỏi và bài tập chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
- Bài tập trắc nghiệm khách quan chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số - Toán 12 Nâng cao
-
CHƯƠNG II. HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3. Lôgarit
- Bài 4. Số e và loogarit tự nhiên
- Bài 5. Hàm số mũ và hàm số lôgarit
- Bài 6. Hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Hệ phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
- Bài tập trắc nghiệm khách quan chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit - Toán 12 Nâng cao
-
CHƯƠNG III. NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
- Bài 1. Nguyên hàm
- Bài 2. Một số phương pháp tìm nguyên hàm
- Bài 3. Tích phân
- Bài 4. Một số phương pháp tích phân
- Bài 5. Ứng dụng tích phân để tính diện tích hình phẳng
- Bài 6. Ứng dụng tích phân để tính thể tích vật thể
- Ôn tập chương III - Nguyên hàm, tích phân và ứng dụng
- Bài tập trắc nghiệm khách quan chương III - Nguyên hàm, tích phân và ứng dụng - Toán 12 Nâng cao
-
CHƯƠNG IV. SỐ PHỨC
-
ÔN TẬP CUỐI NĂM ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 12 NÂNG CAO
-
-
HÌNH HỌC - TOÁN 12 NÂNG CAO
Giải bài tập Toán 12 Nâng cao, Toán 12 Nâng cao, đầy đủ giải tích và hình học
Bài 2. Khối đa diện lồi và khối đa diện đều
Giải bài 3 trang 18 SGK Hình học 12
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
Đề bài
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Sử dụng tính chất đường trung tuyến của tam giác và định lý Ta-lét để làm bài toán.
Lời giải chi tiết
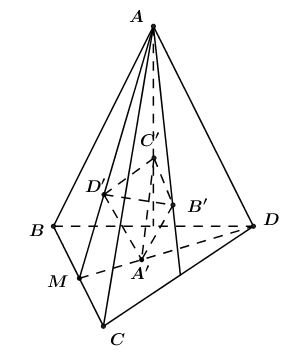
Gọi \(A’, B’, C’, D’\) lần lượt là trọng tâm của các tam giác đều \(BCD, ACD, ABD, ABC\).
Gọi \(M\) là trung điểm \(BC\):
Ta có: \(\dfrac {MD'} {MA} = \dfrac {MA'}{MD} = \dfrac {1} {3}\) (tính chất đường trung tuyến).
\( \Rightarrow A'D'//A{\rm{D}}\) (định lý Ta-lét).
và \(A'D' = \dfrac {1} {3}{AD} = \dfrac {a} {3}\)
Tương tự \(A'B' = B'C' = C'A' = B'D' = C'D' = \dfrac {a} {3}\)
Vậy \(A’B’C’D’\) là tứ diện đều.
Loigiaihay.com
Bình luận
Chia sẻ
- Giải bài 4 trang 18 SGK Hình học 12
- Giải bài 2 trang 18 SGK Hình học 12
- Giải bài 1 trang 18 SGK Hình học 12
- Trả lời câu hỏi 4 trang 18 SGK Hình học 12
- Trả lời câu hỏi 3 trang 17 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
