Câu 9 trang 51 Sách bài tập Hình học 11 nâng cao.

Chứng minh ba điểm M, N, I thẳng hàng.

Đề bài

Cho ba tia Ox, Oy, Oz. Trên các tia Ox, Oy, Oz lần lượt lấy các điểm A và A’, B và B’, C và C’ sao cho BC cắt B’C’ tại M, CA cắt C’A’ tại N và AB cắt A’B’ tại I. Chứng minh ba điểm M, N, I thẳng hàng.

Lời giải chi tiết

Trường hợp Ox, Oy, Oz không đồng phẳng

Dễ thấy M, N, I là ba điểm chung của hai mặt phẳng phân biệt (ABC) và (A’B’C’) nên chúng thuộc giao tuyến của hai mặt phẳng đó. Vậy ba điểm M, N, I thẳng hàng.

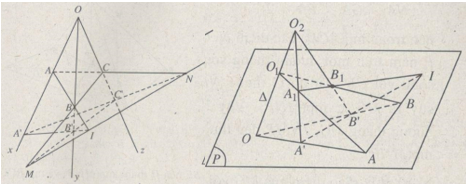
Trường hợp Ox, Oy, Oz thuộc mặt phẳng (P).

Qua O ta dựng một đường thẳng \(\Delta \) không nằm trên mp(P). Trên \(\Delta \) lấy các điểm \({O_1},\,{O_2}.\) Gọi \({A_1}\) là giao điểm của \({O_1}A\) với \({O_2}A',\,{B_1}\) là giao điểm của \({O_1}B\) với \({O_2}B'.\) Dễ chứng minh \({A_1}{B_1},A'B',\,AB\) đồng quy tại I. Tương tự, ta dựng điểm \({C_1}\) là giao điểm của \({O_1}C\) với \({O_2}C'.\) Hai tam giác \({A_1}{B_1}{C_1}\) và ABC không nằm trong một mặt phẳng, nên theo câu a) ta được ba điểm M, N, I thẳng hàng.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.3 trên 4 phiếu

Bài tiếp theo

Câu 10 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm A, B, C, D không đồng phẳng. Gọi I, K theo thứ tự là hai điểm trong của các tam giác ABC và BCD. Giả sử đường thẳng IK cắt mặt phẳng (ACD) tại J. Hãy xác định giao điểm J đó.
Câu 11 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm không đồng phẳng A, B, C, D; G là trọng tâm của tam giác ACD.
Câu 12 trang 52 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD. Trên cạnh SC lấy một điểm E không trùng với hai điểm S và C.
Câu 13 trang 52 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là hình bình hành, O là tâm của đáy; M, N lần lượt là trung điểm của SA, SC. Gọi (P) là mặt phẳng qua M, N và B.
Câu 14 trang 52 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ABCD. Hãy xác định thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (MNI) trong các trường hợp dưới đây.
Câu 15 trang 52 Sách bài tập Hình học 11 nâng cao.
Gọi I, J theo thứ tự là trung điểm của các cạnh SB và SC.
Câu 16 trang 53 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp tứ giác S.ABCD.
Câu 17 trang 53 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện ABCD. Gọi E là điểm đối xứng của A qua điểm C. Xác định thiết diện của hình tứ diện khi cắt bởi mặt phẳng đi qua B, E và một điểm F trong các trường hợp sau đây.
Câu 18 trang 53 Sách bài tập Hình học 11 nâng cao.
Cho hình chóp S.ABCD có đáy là tứ giác lồi. Mặt phẳng (P) đi qua SA và chia đáy hình chóp thành hai phần có diện tích bằng nhau. Hãy xác định thiết diện của hình chóp khi cắt bởi mp(P).
Câu 19 trang 53 Sách bài tập Hình học 11 nâng cao.
Cho tứ diện đều ABCD có cạnh bằng a. Gọi I là trung điểm của AD, J là điểm đối xứng với D qua C, K là điểm đối xứng với D qua B.
Câu 20 trang 53 Sách bài tập Hình học 11 nâng cao.
Chứng minh rằng các đường thẳng đi qua mỗi đỉnh và tâm đường tròn nội tiếp của mặt đối diện đồng quy tại một điểm.
Câu 21 trang 53 Sách bài tập Hình học 11 nâng cao.
Một mặt phẳng (P) thay đổi luôn chứa MN, cắt các cạnh CD và BD lần lượt tại E và F.
Câu 8 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC.
Câu 7 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
Câu 6 trang 51 Sách bài tập Hình học 11 nâng cao.
Chứng minh rằng nếu hai đường thẳng MA, MB lần lượt cắt mp (P) tại hai điểm A’, B’ phân biệt thì đường thẳng A’B’ đi qua một điểm cố định.
Câu 5 trang 51 Sách bài tập Hình học 11 nâng cao.
Chứng minh rằng bốn điểm M, N, I, J không đồng phẳng.
Câu 4 trang 51 Sách bài tập Hình học 11 nâng cao.
Chứng minh rằng n điểm đó đồng phẳng.
Câu 3 trang 51 Sách bài tập Hình học 11 nâng cao.
Chứng minh rằng không có ba điểm nào trong chúng thẳng hàng.
Câu 2 trang 51 Sách bài tập Hình học 11 nâng cao.
Cho mặt phẳng (P) và ba điểm A, B, C nằm ngoài mp (P). Giả sử đoạn thẳng AB và đoạn thẳng BC đều cắt mp (P). Chứng minh rằng đoạn thẳng AC không cắt mp (P).
Câu 1 trang 51 Sách bài tập Hình học 11 nâng cao.
Chứng minh rằng: Một mặt phẳng và một đường thẳng không nằm trên mặt phẳng đó có không quá một điểm chung.