Giải SBT toán hình học và đại số 11 nâng cao Bài 1: Đại cương về đường thẳng và mặt phẳng

Câu 19 trang 53 Sách bài tập Hình học 11 nâng cao.


Cho tứ diện đều ABCD có cạnh bằng a. Gọi I là trung điểm của AD, J là điểm đối xứng với D qua C, K là điểm đối xứng với D qua B.

Đề bài

Cho tứ diện đều ABCD có cạnh bằng a. Gọi I là trung điểm của AD, J là điểm đối xứng với D qua C, K là điểm đối xứng với D qua B.

a) Xác định thiết diện của hình tứ diện khi cắt bởi mp(IJK).

b) Tính diện tích thiết diện được xác định bởi câu a.

Lời giải chi tiết

a) Nối I và J cắt AC tại N. Nối I và K cắt AB tại M. Tam giác IMN là thiết diện cần tìm.

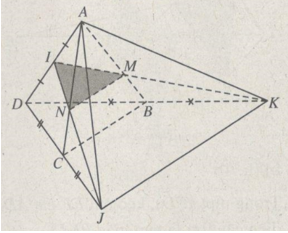
b) Dễ thấy M là trọng tâm tam giác ADK, N là trọng tâm tam giác ADJ. Từ đó ta có:

\(AN = {2 \over 3}AC;\;AM = {2 \over 3}AB\)

Suy ra: \(AN = AM = {2 \over 3}a\) và MN//CB. Do đó \(MN = {2 \over 3}CB\)

hay \(MN = {2 \over 3}a.\)

Xét tam giác AIM. Ta có:

\(\eqalign{
& I{M^2} = A{I^2} + A{M^2} - 2AI.AM.\cos {60^o} \cr 
& \,\,\,\,\,\,\,\,\,\,\, = {{{a^2}} \over 4} + {4 \over 9}{a^2} - 2.{a \over 2}.{{2a} \over 3}.{1 \over 2} = {{13} \over {36}}{a^2} \cr 
& \Rightarrow IM = {{a\sqrt {13} } \over 6} \cr} \)

Tương tự, ta có \(IN = {{a\sqrt {13} } \over 6}\)

Vậy theo công thức Hê-rông, ta có:

\({S_{IMN}} = \sqrt {\left( {{{a\sqrt {13} } \over 6} + {2 \over 6}a} \right).{2 \over 6}a.{2 \over 6}a.\left( {{{a\sqrt {13} } \over 6} - {2 \over 6}a} \right)} \)

            \(= {{{a^2}} \over 6}.\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store